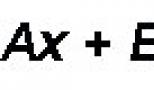Формули площин. Рівняння площини: загальне, через три точки, нормальне. Відстань від точки до площини

Щоб отримати загальне рівняння площини, розберемо площину, що проходить через задану точку.

Нехай в просторі є три вже відомі нам осі координат - Ox, Oy і Oz. Потримаємо аркуш паперу так, щоб він залишався плоским. Площиною буде сам лист і його продовження у всіх напрямках.

нехай P довільна площина в просторі. Всякий перпендикулярний їй вектор називається вектором нормалі до цієї площини. Природно, мова йде про ненулевом векторі.

Якщо відома якась точка площині P і який-небудь вектор нормалі до неї, то цими двома умовами площину в просторі цілком визначена (Через задану точку можна провести єдину площину, перпендикулярну даному вектору). Загальне рівняння площини буде мати вигляд:

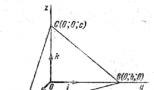
Отже, умови, якими задається рівняння площині, є. Щоб отримати саме рівняння площини, Що має наведений вище вид, візьмемо на площині P довільну точку M зі змінними координатами x, y, z. Ця точка належить площині тільки в тому випадку, коли вектор перпендикулярний вектору (Рис. 1). Для цього, згідно з умовою перпендикулярності векторів, необхідно і достатньо, щоб скалярний добуток цих векторів дорівнювало нулю, тобто

Вектор заданий за умовою. Координати вектора знайдемо за формулою :

.

Тепер, використовуючи формулу скалярного твори векторів , Висловимо скалярний твір в координатної формі:

Так як точка M (x; y; z) обрана на площині довільно, то останнім рівнянням задовольняють координати будь-якої точки, що лежить на площині P. для точки N, Що не лежить на заданій площині,, тобто рівність (1) порушується.

Приклад 1. Скласти рівняння площини, що проходить через точку і перпендикулярної вектору.

Рішення. Використовуємо формулу (1), ще раз подивимося на неї:

У цій формулі числа A , B і C координати вектора, а числа x0 , y0 і z0 - координати точки.

Обчислення дуже прості: підставляємо ці числа в формулу і отримуємо

Множимо все, що потрібно помножити і складаємо просто числа (які без букв). результат:

.

Необхідну рівняння площини в цьому прикладі виявилося виражено загальним рівнянням першого ступеня щодо змінних координат x, y, z довільної точки площини.

Отже, рівняння виду

називається загальним рівнянням площини .

Приклад 2.Побудувати в прямокутній декартовій системі координат площину, задану рівнянням .

Рішення. Для побудови площини необхідно і достатньо знати будь-які три її точки, що не лежать на одній прямій, наприклад, точки перетину площини з осями координат.

Як знайти ці точки? Щоб знайти точку перетину з віссю Oz , Потрібно в рівняння, дане в умові завдання, замість ікс і Ігрека підставити нулі: x = y \u003d 0. Тому отримуємо z \u003d 6. Таким чином, задана площина перетинає вісь Oz в точці A(0; 0; 6) .

Точно так же знаходимо точку перетину площини з віссю Oy . при x = z \u003d 0 отримуємо y \u003d -3, тобто точку B(0; −3; 0) .

І, нарешті, знаходимо точку перетину нашої площині з віссю Ox . при y = z \u003d 0 отримаємо x \u003d 2, тобто точку C(2; 0; 0). З трьох отриманим в нашому рішенні точкам A(0; 0; 6) , B(0; -3; 0) і C(2; 0; 0) будуємо задану площину.

Розглянемо тепер окремі випадки загального рівняння площини. Це випадки, коли ті чи інші коефіцієнти рівняння (2) звертаються в нуль.

1. При D \u003d0 рівняння визначає площину, що проходить через початок координат, так як координати точки 0 (0; 0; 0) задовольняють цьому рівнянню.

2. При A \u003d0 рівняння визначає площину, паралельну осі Ox, Оскільки вектор нормалі цій площині перпендикулярний осі Ox (Його проекція на вісь Ox дорівнює нулю). Аналогічно, при B \u003d0 площину паралельна осі Oy, А при C \u003d0 площину паралельна осі Oz.

3. При A \u003d D \u003d 0 рівняння визначає площину, що проходить через вісь Ox, Оскільки вона паралельна осі Ox (A \u003dD \u003d 0). Аналогічно, площина проходить через вісь Oy, А площину через вісь Oz.

4. При A \u003d B \u003d0 рівняння визначає площину, паралельну координатної площини xOy, Оскільки вона паралельна осях Ox (A \u003d 0) і Oy (B \u003d 0). Аналогічно, площина паралельна площині yOz, А площину - площині xOz.

5. При A \u003d B \u003d D \u003d0 рівняння (або z \u003d0) визначає координатну площину xOy, Так як вона паралельна площині xOy (A \u003d B \u003d 0) і проходить через початок координат ( D \u003d0). Аналогічно, рівняння y \u003d0 в просторі визначає координатну площину xOz, А рівняння x \u003d0 - координатну площину yOz.

Приклад 3. Скласти рівняння площини P , Що проходить через вісь Oy і точку.

Рішення. Отже, площина проходить через вісь Oy . Тому в її рівнянні y \u003d 0 і це рівняння має вигляд. Для визначення коефіцієнтів A і C скористаємося тим, що точка належить площині P .

Тому серед її координат є такі, які можна підставити в рівняння площини, яке ми вже вивели (). Дивимося ще раз на координати точки:

M0 (2; −4; 3) .

Серед них x = 2 , z \u003d 3. Підставляємо їх в рівняння загального вигляду і отримуємо рівняння для нашого окремого випадку:

2A + 3C = 0 .

Ми залишаємо 2 A в лівій частині рівняння, переносимо 3 C в праву частину і отримуємо

A = −1,5C .

Підставивши знайдене значення A в рівняння, отримаємо

або.

Це і є рівняння, необхідне в умові прикладу.

Вирішити завдання на рівняння площини самостійно, а потім подивитися рішення

Приклад 4. Визначити площину (або площини, якщо більше однієї) щодо координатних осей або координатних площин, якщо площину (площині) задана рівнянням.

Рішення типових задач, які бувають на контрольних роботах - в посібнику "Завдання на площину: паралельність, перпендикулярність, перетин трьох площин в одній точці".

Рівняння площини, що проходить через три точки

Як уже згадувалося, необхідною і достатньою умовою для побудови площини, крім однієї точки і вектора нормалі, є також три точки, що не лежать на одній прямій.

Нехай дано три різні точки, і, що не лежать на одній прямій. Оскільки вказані три точки не лежать в одній прямий, вектори і не колінеарні, а тому будь-яка точка площині лежить в одній площині з точками, і тоді і тільки тоді, коли вектори, і компланарність, тобто тоді і тільки тоді, коли мішаний добуток цих векторів дорівнює нулю.

Використовуючи вираз змішаного твори в координатах, отримаємо рівняння площини

(3)

Після розкриття визначника це рівняння стає рівнянням виду (2), тобто загальним рівнянням площини.

Приклад 5. Скласти рівняння площини, що проходить через три дані точки, що не лежать на одній прямій:

і визначити окремий випадок загального рівняння прямої, якщо такий має місце.

Рішення. За формулою (3) маємо:

Нормальне рівняння площині. Відстань від точки до площини

Нормальним рівнянням площини називається її рівняння, записане у вигляді

1. Загальне рівняння площини

Визначення. Площиною називається поверхню, всі точки якої задовольняють загальним рівнянням: Ax + By + Cz + D \u003d 0, де А, В, С - координати вектора

N \u003d Ai + Bj + Ck вектор нормалі до площини. Можливі такі окремі випадки:

A \u003d 0 - площина паралельна осі Ох

B \u003d 0 - площина паралельна осі Оу C \u003d 0 - площина паралельна осі Оz

D \u003d 0 - площина проходить через початок координат

A \u003d B \u003d 0 - площина паралельна площині хОу A \u003d C \u003d 0 - площина паралельна площині хОz B \u003d C \u003d 0 - площина паралельна площині yOz A \u003d D \u003d 0 - площина проходить через вісь Ох

B \u003d D \u003d 0 - площина проходить через вісь Оу C \u003d D \u003d 0 - площина проходить через вісь Oz

A \u003d B \u003d D \u003d 0 - площина збігається з площиною хОу A \u003d C \u003d D \u003d 0 - площина збігається з площиною xOz B \u003d C \u003d D \u003d 0 - площина збігається з площиною yOz

2. Рівняння поверхні в просторі

Визначення. Будь-яке рівняння, що зв'язує координати x, y, z будь-якої точки поверхні є рівнянням цієї поверхні.

3. Рівняння площини, що проходить через три точки

Для того, щоб через три какиелибо точки простору можна було провести єдину площину, необхідно, щоб ці точки не лежали на одній прямій.

Розглянемо точки М1 (x1, y1, z1), M2 (x2, y2, z2), M3 (x3, y3, z3) в загальній декартовій системі

4. Рівняння площини по двох точках і вектору, колінеарну площині

Нехай задані точки М1 (x1, y1, z1), M2 (x2, y2, z2) і векторa \u003d (a 1, a 2, a 3).

Складемо рівняння площини, що проходить через дані точки М1 і М2 і довільну

5. Рівняння площини по одній точці і двох векторах, колінеарну площині

Нехай задані два вектори a \u003d (a 1, a 2, a 3) і b \u003d (b 1, b 2, b 3), Колінеарні площині. Тоді для довільної точки М (х, у, z), що належить площині, вектори a, b, MM 1 повинні бути компланарність.

6. Рівняння площини по точці і вектору нормалі

Теорема. Якщо в просторі задана точка M 0 (x 0, y 0, z 0), то рівняння площини, що проходить через точку M 0 перпендикулярно вектору нормалі N (A, B, C) має вигляд: A (x - x 0) + B (y - y 0) + C (z - z 0) \u003d 0.

7. Рівняння площини у відрізках

Якщо в загальному рівнянні Ax + By + Cz + D \u003d 0 поділити обидві частини на (-D)

з осями х, у, z.

8. Рівняння площини у векторній формі

r n \u003d p, де r \u003d xi + yj + zk - радіусвектор поточної точки M (x, y, z),

n \u003d i cosα + j cos β + k cosγ - одиничний вектор, який має напрямок, перпендикуляра,

опущеного на площину з початку координат. α, β і γ - кути, утворені цим вектором з осями х, у, z. p - довжина цього перпендикуляра. У координатах це рівняння має вигляд:

x cosα + y cos β + z cosγ - p \u003d 0

9. Відстань від точки до площини

Відстань від довільної точки M 0 (x 0, y 0, z 0) до площини Ax + By + Cz + D \u003d 0 дорівнює:

d \u003d Ax0 + By0 + Cz0 + D

A2 + B2 + C 2

Приклад. Знайти рівняння площини, що проходить через точки А (2, -1,4) і В (3,2, -1) перпендикулярно площині x + y + 2z - 3 \u003d 0.

Шукане рівняння площини має вигляд: Ax + By + Cz + D \u003d 0, вектор нормалі до цієї площини n 1 (A, B, C). Вектор AB (1,3, -5) належить площині. Задана нам площину,

перпендикулярна шуканої має вектор нормалі n 2 (1,1,2). Оскільки точки А і В належать обом площинам, а площині взаємно перпендикулярні, то

Таким чином, вектор нормалі n 1 (11, -7, -2). Оскільки точка А належить шуканої площини, то її координати повинні задовольняти рівняння цієї площини, тобто

11.2 + 7.1 2.4 + D \u003d 0; D \u003d - 21. Разом, отримуємо рівняння площині: 11x - 7 y - 2z - 21 \u003d 0

10. Рівняння лінії в просторі

Як на площині, так і в просторі, будь-яка лінія може бути визначена як сукупність точок, координати яких в деякій обраної в просторі системі координат задовольняють рівняння:

F (x, y, z) \u003d 0. Це рівняння називається рівнянням лінії в просторі.

Крім того, лінія в просторі може бути визначена й інакше. Її можна розглядати як лінію перетину двох поверхонь, кожна з яких задана какимлибо рівнянням.

Нехай F (x, y, z) \u003d 0 і Ф (x, y, z) \u003d 0 - рівняння поверхонь, що перетинаються по лінії L.

F (x, y, z) \u003d 0

Тоді пару рівнянь Ф (x, y, z) \u003d 0 назвемо рівнянням лінії в просторі.

11. Рівняння прямої в просторі по точці і направляючої векторуr 0 \u003d M 0 M.

Оскільки вектори М 0 М і S колінеарні, то правильне співвідношення М 0 М \u003d \u200b\u200bSt, де t - деякий параметр. Разом, можна записати: r \u003d r 0 + St.

Оскільки цього рівняння задовольняють координати будь-якої точки прямої, то отримане рівняння - параметричне рівняння прямої.

x \u003d x0 + mt

Це векторне рівняння може бути представлене в координатної формі: y \u003d y 0 + nt

z \u003d z0 + pt

Перетворивши цю систему і прирівнявши значення параметра t, отримуємо канонічні

Визначення. Напрямними косинусами прямий називаються напрямні косинуси вектора S, які можуть бути обчислені за формулами:

Звідси отримаємо: m: n: p \u003d cosα: cos β: cosγ.

Числа m, n, p називаються кутовими коефіцієнтами прямий. Оскільки S - ненульовий вектор, то m, n і p не можуть дорівнювати нулю одночасно, але одне або два з цих чисел можуть дорівнювати нулю. В цьому випадку в рівнянні прямої слід прирівняти нулю відповідні числители.

12. Рівняння прямої в просторі, що проходить через дві точки

Якщо на прямій в просторі відзначити дві довільні точки M 1 (x 1, y 1, z 1) і

M 2 (x 2, y 2, z 2), то координати цих точок повинні задовольняти отриманому вище рівняння прямої:

Розглянемо в просторі площину Q. Положення її цілком визначається завданням вектора N, перпендикулярного цій площині, і деякої фіксованої точки лежить в площині Q. Вектор N, перпендикулярний площині Q, називається нормальним вектором цієї площини. Якщо позначити через А, В і С проекції нормального вектора N, то

Виведемо рівняння площині Q, що проходить через дану точку і має даний нормальний вектор. Для цього розглянемо вектор з'єднує точку з довільною точкою площині Q (рис. 81).

При будь-якому положенні точки М на площині Q вектор МХМ перпендикулярний нормальному вектору N площині Q. Тому скалярний твір Запишемо скалярний твір через проекції. Так як, а вектор, то

і, отже,

Ми показали, що координати будь-якої точки площини Q задовольняють рівняння (4). Неважко помітити, що координати точок, які не лежать на площині Q, цього рівняння не задовольняють (в останньому випадку). Отже, нами отримано дані рівняння площини Q. Рівняння (4) називається рівнянням площини, що проходить через дану точку. Воно першого ступеня щодо поточних координат

Отже, ми показали, що будь-якої площини відповідає рівняння першого ступеня щодо поточних координат.

Приклад 1. Написати рівняння площини, що проходить через точку перпендикулярно вектору.

Рішення. Тут. На підставі формули (4) отримаємо

або, після спрощення,

Надаючи коефіцієнтам А, В і С рівняння (4) різні значення, ми можемо отримати рівняння будь-якій площині, що проходить через точку. Сукупність площин, що проходять через дану точку, називається зв'язкою площин. Рівняння (4), в якому коефіцієнти А, В і С можуть приймати будь-які значення, називаються рівнянням зв'язки площин.

Приклад 2. Скласти рівняння площини, що проходить через три точки, (рис. 82).

Рішення. Напишемо рівняння зв'язки площин, що проходять через точку

Можна задавати різними способами (однією точкою і вектором, двома точками і вектором, трьома крапками і ін.). Саме з огляду на це рівняння площині може мати різні види. Також при дотриманні певних умов площині можуть бути паралельними, перпендикулярними, пересічними і т.д. Про це і поговоримо в даній статті. Ми навчимося складати загальне рівняння площини і не тільки.

Нормальний вид рівняння

Припустимо, є простір R 3, яке має прямокутну координатну систему XYZ. Задамо вектор α, який буде випущений з початкової точки О. Через кінець вектора α проведемо площину П, яка буде йому перпендикулярна.

Позначимо на П довільну точку Q \u003d (х, у, z). Радіус-вектор точки Q підпишемо буквою р. При цьому довжина вектора α дорівнює р \u003d IαI і Ʋ \u003d (cosα, cosβ, cosγ).

Це одиничний вектор, який направлений в сторону, як і вектор α. α, β і γ - це кути, які утворюються між вектором Ʋ і позитивними напрямками осей простору х, у, z відповідно. Проекція будь-якої точки QεП на вектор Ʋ є постійною величиною, яка дорівнює р: (р, Ʋ) \u003d р (р≥0).

Зазначене рівняння має сенс, коли р \u003d 0. Єдине, площину П в цьому випадку буде перетинати точку О (α \u003d 0), яка є початком координат, і одиничний вектор Ʋ, випущений з точки О, буде перпендикулярний до П, незважаючи на його напрямок, що означає, що вектор Ʋ визначається з точністю до знака. Попереднє рівняння є рівнянням нашої площині П, вираженим у векторній формі. А ось в координатах його вид буде таким:

Р тут більше або дорівнює 0. Ми знайшли рівняння площини в просторі в нормальному вигляді.

загальне рівняння

Якщо рівняння в координатах помножимо на будь-яке число, яке не дорівнює нулю, отримаємо рівняння, еквівалентне даному, що визначає ту саму площину. Воно буде мати такий вигляд:

Тут А, В, С - це числа, одночасно відмінні від нуля. Це рівняння називається як рівняння площини загального вигляду.

Рівняння площин. окремі випадки

Рівняння в загальному вигляді може видозмінюватися при наявності додаткових умов. Розглянемо деякі з них.

Припустимо, що коефіцієнт А дорівнює 0. Це означає, що дана площину паралельна заданій осі Ох. У цьому випадку вид рівняння зміниться: Ву + Cz + D \u003d 0.

Аналогічно вид рівняння буде змінюватися і за таких умов:

• По-перше, якщо В \u003d 0, то рівняння зміниться на Ах + Cz + D \u003d 0, що свідчитиме про паралельність до осі Оу.
• По-друге, якщо С \u003d 0, то рівняння перетворюється в Ах + Ву + D \u003d 0, що буде говорити про паралельність до заданої осі Oz.
• По-третє, якщо D \u003d 0, рівняння буде виглядати як Ах + Ву + Cz \u003d 0, що буде означати, що площина перетинає О (початок координат).
• По-четверте, якщо A \u003d B \u003d 0, то рівняння зміниться на Cz + D \u003d 0, що буде доводити паралельність до Oxy.
• По-п'яте, якщо B \u003d C \u003d 0, то рівняння стане Ах + D \u003d 0, а це означає, що площина до Oyz паралельна.
• По-шосте, якщо A \u003d C \u003d 0, то рівняння набуде вигляду Ву + D \u003d 0, тобто буде повідомляти про паралельність до Oxz.

Вид рівняння у відрізках

У разі коли числа А, В, С, D відмінні від нуля, вид рівняння (0) може бути наступним:

х / а + у / b + z / с \u003d 1,

в якому а \u003d -D / А, b \u003d -D / В, з \u003d -D / С.

Отримуємо в результаті Варто відзначити, що дана площину буде перетинати вісь Ох у точці з координатами (а, 0,0), Оу - (0, b, 0), а Oz - (0,0, с).

З урахуванням рівняння х / а + у / b + z / с \u003d 1 неважко візуально уявити розміщення площині щодо заданої координатної системи.

Координати нормального вектора

Нормальний вектор n до площини П має координати, які є коефіцієнтами загального рівняння даної площини, тобто n (А, В, С).

Для того щоб визначити координати нормалі n, досить знати загальне рівняння заданої площині.

При використанні рівняння у відрізках, яке має вигляд х / а + у / b + z / с \u003d 1, як і при використанні загального рівняння, можна записати координати будь-якого нормального вектора заданої площині: (1 / а + 1 / b + 1 / с).

Варто відзначити, що нормальний вектор допомагає вирішити різноманітні завдання. До найпоширеніших належать завдання, які полягають в доказі перпендикулярності або паралельності площин, завдання по знаходженню кутів між площинами або кутів між площинами і прямими.

Вид рівняння площини згідно координатам точки і нормального вектора

Ненульовий вектор n, перпендикулярний заданій площині, називають нормальним (нормаллю) для заданої площині.

Припустимо, що в координатному просторі (прямокутної системі координат) Oxyz задані:

• точка Мₒ з координатами (хₒ, уₒ, zₒ);
• нульовий вектор n \u003d А * i + В * j + С * k.

Потрібно скласти рівняння площини, яка буде проходити через точку Мₒ перпендикулярно нормалі n.

У просторі виберемо будь-яку довільну точку і позначимо її М (х у, z). Нехай радіус-вектор будь-якої точки М (х, у, z) буде r \u003d х * i + у * j + z * k, а радіус-вектор точки Мₒ (хₒ, уₒ, zₒ) - rₒ \u003d хₒ * i + уₒ * j + zₒ * k. Точка М буде належати заданої площині, якщо вектор МₒМ буде перпендикулярний вектору n. Запишемо умову ортогональності за допомогою скалярного твори:

[МₒМ, n] \u003d 0.

Оскільки МₒМ \u003d r-rₒ, векторне рівняння площини виглядати буде так:

Дане рівняння може мати й іншу форму. Для цього використовуються властивості скалярного твори, а перетворюється ліва сторона рівняння. \u003d -. Якщо позначити як з, то вийде наступне рівняння: - з \u003d 0 або \u003d с, яке виражає сталість проекцій на нормальний вектор радіус-векторів заданих точок, які належать площині.

Тепер можна отримати координатний вид запису векторного рівняння нашої площині \u003d 0. Оскільки r-rₒ \u003d (х-хₒ) * i + (у-уₒ) * j + (z-zₒ) * k, а n \u003d А * i + В * j + С * k, ми маємо:

Виходить, у нас утворюється рівняння площини, що проходить через точку перпендикулярно нормалі n:

А * (х- хₒ) + В * (у-уₒ) С * (z-zₒ) \u003d 0.

Вид рівняння площини згідно координатам двох точок і вектора, колінеарну площині

Задамо дві довільні точки М '(х', у ', z') і М "(х", у ", z"), а також вектор а (а ', а ", а ‴).

Тепер ми зможемо скласти рівняння заданої площині, яка буде проходити через наявні точки М 'і М ", а також будь-яку точку М з координатами (х, у, z) паралельно заданому вектору а.

При цьому вектори М'М \u003d (х-х '; у-у'; zz ') і М "М \u003d (х" х'; у "-у '; z" -z') повинні бути компланарними з вектором а \u003d (а ', а ", а ‴), а це означає, що (М'М, М" М, а) \u003d 0.

Отже, наше рівняння площини в просторі буде виглядати так:

Вид рівняння площині, що перетинає три точки

Припустимо, у нас є три точки: (х ', у', z '), (х ", у", z "), (х ‴, у ‴, z ‴), які не належать одній прямій. Необхідно написати рівняння площини, що проходить через задані три точки. Теорія геометрії стверджує, що такого роду площину дійсно існує, ось тільки вона єдина і неповторна. Оскільки ця площина перетинає точку (х ', у', z '), вид її рівняння буде таким:

Тут А, В, С відмінні від нуля одночасно. Також задана площина перетинає ще дві точки: (х ", у", z ") і (х ‴, у ‴, z ‴). У зв'язку з цим повинні виконуватися такого роду умови:

Зараз ми можемо скласти однорідну систему з невідомими u, v, w:

У нашому випадку х, у або z виступає довільної точкою, яка задовольняє рівняння (1). З огляду на рівняння (1) і систему з рівнянь (2) і (3), системі рівнянь, зазначеної на малюнку вище, задовольняє вектор N (А, В, С), який є нетривіальним. Саме тому визначник даної системи дорівнює нулю.

Рівняння (1), яке у нас вийшло, це і є рівняння площині. Через 3 точки вона точно проходить, і це легко перевірити. Для цього потрібно розкласти наш визначник за елементами, що знаходяться в першому рядку. З існуючих властивостей визначника випливає, що наша площину одночасно перетинає три спочатку задані точки (х ', у', z '), (х ", у", z "), (х ‴, у ‴, z ‴). Тобто ми вирішили поставлене перед нами завдання.

Двухгранний кут між площинами

Двухгранний кут є просторовою геометричну фігуру, утворену двома півплощини, які виходять з однієї прямої. Іншими словами, це частина простору, яка обмежується даними напівплощиною.

Припустимо, у нас є дві площини з наступними рівняннями:

Нам відомо, що вектори N \u003d (А, В, С) і N¹ \u003d (А¹, В¹, С¹) перпендикулярні згідно із заданими площинах. У зв'язку з цим кут φ між векторами N і N¹ дорівнює розі (двухгранний), який знаходиться між цими площинами. Скалярний твір має вигляд:

NN¹ \u003d | N || N¹ | cos φ,

саме тому

cosφ \u003d NN¹ / | N || N¹ | \u003d (АА¹ + ВВ¹ + СС¹) / ((√ (А ² + В² + с?)) * (√ (А¹) ² + (В¹) ² + (С¹) ²)).

Досить врахувати, що 0≤φ≤π.

Насправді дві площини, які перетинаються, утворюють два кута (двухгранних): φ 1 і φ 2. Сума їх дорівнює π (φ 1 + φ 2 \u003d π). Що стосується їх косинусів, то їх абсолютні величини рівні, але розрізняються вони знаками, тобто cos φ 1 \u003d -cos φ 2. Якщо в рівнянні (0) замінити А, В і С на числа -А, -В і -С відповідно, то рівняння, яке ми отримаємо, буде визначати цю ж площину, єдине, кут φ в рівнянні cos φ \u003d NN 1 / | N || N 1 | буде замінений на π-φ.

Рівняння перпендикулярній площині

Перпендикулярними називаються площині, між якими кут дорівнює 90 градусів. Використовуючи матеріал, викладений вище, ми можемо знайти рівняння площини, перпендикулярної інший. Припустимо, у нас є дві площини: Ах + Ву + Cz + D \u003d 0 і А¹х + В¹у + С¹z + D \u003d 0. Ми можемо стверджувати, що перпендикулярними вони будуть, якщо cosφ \u003d 0. Це означає, що NN¹ \u003d АА¹ + ВВ¹ + СС¹ \u003d 0.

Рівняння паралельній площині

Паралельними називаються дві площини, які не містять спільних точок.

Умова (їх рівняння ті ж, що і в попередньому пункті) полягає в тому, що вектори N і N¹, які до них перпендикулярні, Колінеарні. А це значить, що виконуються наступні умови пропорційності:

А / А¹ \u003d В / В¹ \u003d С / С¹.

Якщо умови пропорційності є розширеними - А / А¹ \u003d В / В¹ \u003d С / С¹ \u003d DD¹,

це свідчить про те, що дані площини збігаються. А це означає, що рівняння Ах + Ву + Cz + D \u003d 0 і А¹х + В¹у + С¹z + D¹ \u003d 0 описують одну площину.

Відстань до площини від точки

Припустимо, у нас є площину П, яка задана рівнянням (0). Необхідно знайти до неї відстань від точки з координатами (хₒ, уₒ, zₒ) \u003d Qₒ. Щоб це зробити, потрібно привести рівняння площини П в нормальний вигляд:

(Ρ, v) \u003d р (р≥0).

В даному випадку ρ (х, у, z) є радіус-вектором нашої точки Q, розташованої на П, р - це довжина перпендикуляра П, який був випущений з нульової точки, v - це одиничний вектор, який розташований в напрямку а.

Різниця ρ-ρº радіус-вектора який-небудь точки Q \u003d (х, у, z), що належить П, а також радіус-вектора заданої точки Q 0 \u003d (хₒ, уₒ, zₒ) є таким вектором, абсолютна величина проекції якого на v дорівнює відстані d, яке потрібно знайти від Q 0 \u003d (хₒ, уₒ, zₒ) до П:

D \u003d | (ρ-ρ 0, v) |, але

(Ρ-ρ 0, v) \u003d (ρ, v) - (ρ 0, v) \u003d р- (ρ 0, v).

Ось і виходить,

d \u003d | (ρ 0, v) -р |.

Таким чином, ми знайдемо абсолютне значення отриманого виразу, тобто шукане d.

Використовуючи мову параметрів, отримуємо очевидне:

d \u003d | Ахₒ + Вуₒ + Czₒ | / √ (А ² + В² + с?).

Якщо задана точка Q 0 знаходиться по іншу сторону від площини П, як і початок координат, то між вектором ρ-ρ 0 і v знаходиться отже:

d \u003d - (ρ-ρ 0, v) \u003d (ρ 0, v) -р\u003e 0.

У разі коли точка Q 0 спільно з початком координат розташовується по одну і ту ж сторону від П, то створюваний кут гострий, тобто:

d \u003d (ρ-ρ 0, v) \u003d р - (ρ 0, v)\u003e 0.

У підсумку виходить, що в першому випадку (ρ 0, v)\u003e р, у другому (ρ 0, v)<р.

Дотична площину і її рівняння

Що стосується площину до поверхні в точці дотику мº - це площина, яка містить всі можливі дотичні до кривих, проведеним через цю точку на поверхні.

При такому вигляді рівняння поверхні F (х, у, z) \u003d 0 рівняння дотичної площини в дотичній точці мº (хº, уº, zº) буде виглядати так:

F х (хº, уº, zº) (х- хº) + F х (хº, уº, zº) (у-уº) + F х (хº, уº, zº) (z-zº) \u003d 0.

Якщо задати поверхню в явній формі z \u003d f (х, у), то дотична площину буде описана рівнянням:

z-zº \u003d f (хº, уº) (х- хº) + f (хº, уº) (у-уº).

Перетин двох площин

В розташована система координат (прямокутна) Oxyz, дано дві площини П 'і П ", які перетинаються і не збігаються. Оскільки будь-яка площина, що знаходиться в прямокутній системі координат, визначається загальним рівнянням, будемо вважати, що П 'і П "задаються рівняннями А'х + В'у + С'z + D' \u003d 0 і А" х + В "у + З "z + D" \u003d 0. У такому випадку маємо нормаль n '(А', В ', С') площині П 'і нормаль n "(А", В ", С") площині П ". Оскільки наші площині не паралельні і не збігаються, то ці вектори не є колінеарними. Використовуючи мову математики, ми цю умову можемо записати так: n '≠ n "↔ (А', В ', С') ≠ (λ * А", λ * В ", λ * С"), λεR. Нехай пряма, яка лежить на перетині П 'і П ", буде позначатися літерою а, в цьому випадку а \u003d П' ∩ П".

а - це пряма, що складається з безлічі всіх точок (загальних) площин П 'і П ". Це означає, що координати будь-якої точки, що належить прямій а, повинні одночасно задовольняти рівняння А'х + В'у + С'z + D '\u003d 0 і А "х + В" у + С "z + D" \u003d 0. Значить, координати точки будуть приватним рішенням наступної системи рівнянь:

У підсумку виходить, що рішення (загальне) цієї системи рівнянь буде визначати координати кожної з точок прямої, яка буде виступати точкою перетину П 'і П ", і визначати пряму а в системі координат Oxyz (прямокутної) в просторі.

Нормальне рівняння площині.

Загальне рівняння площини виду називають нормальним рівнянням площини, Якщо довжина вектора дорівнює одиниці, тобто, , І.

Часто можна бачити, що нормальне рівняння площині записують у вигляді. Тут - напрямні косинуси нормального вектора цій площині одиничної довжини, тобто, а p - невід'ємне число, рівне відстані від початку координат до площини.

Нормальне рівняння площини в прямокутній системі координат Oxyz визначає площину, яка віддалена від початку координат на відстань p в позитивному напрямку нормального вектора цієї площини . якщо p \u003d 0, То площину проходить через початок координат.

Наведемо приклад нормального рівняння площині.

Нехай площину задана в прямокутній системі координат Oxyz загальним рівняння площини виду . Це загальне рівняння площини є нормальним рівнянням площини. Дійсно, і нормальний вектор цієї площини має довжину рівну одиниці, так як .

Рівняння площини в нормальному вигляді дозволяє знаходити відстань від точки до площини.

Відстань від точки до площини.

Відстань від точки до площини - це найменше з відстаней між цією точкою і точками площини. Відомо що відстань від точки до площини дорівнює довжині перпендикуляра, опущеного з цієї точки на площину.

Якщо і початок координат лежать по різні боки площини, в протилежному випадку. Відстань від точки до площини дорівнює

Взаємне розташування площин. Умови паралельності і перпендикулярності площин.

Відстань між паралельними площинами

пов'язані поняття

площині паралельні , якщо

або (Векторний витвір)

площині перпендикулярні, якщо

або . (Скалярний твір)

Пряма в просторі. Різні види рівняння прямої.

Рівняння прямої в просторі - початкові відомості.

Рівняння прямої на площині Oxy являє собою лінійне рівняння з двома змінними x і y, Якому задовольняють координати будь-якої точки прямої і не задовольняють координати ніяких інших точок. З прямої в тривимірному просторі справа йде трохи інакше - не існує лінійного рівняння з трьома змінними x, y і z, Якому б задовольняли лише координати точок прямої, заданої в прямокутній системі координат Oxyz. Дійсно, рівняння виду, де x, y і z - змінні, а A, B, C і D - деякі дійсні числа, причому А, В і З одночасно не рівні нулю, являє собою загальне рівняння площини. Тоді постає питання: «Яким же чином можна описати пряму лінію в прямокутній системі координат Oxyz»?

Відповідь на нього міститься в наступних пунктах статті.

Рівняння прямої в просторі - це рівняння двох пересічних площин.

Нагадаємо одну аксіому: якщо дві площини в просторі мають спільну точку, то вони мають загальну пряму, на якій знаходяться всі загальні точки цих площин. Таким чином, пряму лінію в просторі можна задати, вказавши дві площини, що перетинаються по цій прямій.

Переведемо останнє твердження на мову алгебри.

Нехай в тривимірному просторі зафіксована прямокутна система координат Oxyz і відомо, що пряма a є лінією перетину двох площин і, яким відповідають загальні рівняння площини відаісоответственно. Так як пряма a являє собою безліч всіх спільних точок площин і, то координати будь-якої точки прямої a будуть задовольняти одночасно і уравненіюі рівняння, координати ніяких інших точок не будуть задовольняти одночасно обом рівнянням площин. Отже, координати будь-якої точки прямої a в прямокутній системі координат Oxyz являють собою приватне рішення системи лінійних рівнянь виду , А загальне рішення системи рівнянь визначає координати кожної точки прямої a, Тобто, визначає пряму a.

Отже, пряма в просторі в прямокутній системі координат Oxyz може бути задана системою з рівнянь двох пересічних площин .

Ось приклад завдання прямої лінії в просторі за допомогою системи двох рівнянь - .

Опис прямій лінії рівняннями двох пересічних площин відмінно підходить при знаходженні координат точки перетину прямої і площини, А також при знаходженні координат точки перетину двох прямих у просторі.

Рекомендуємо продовжити вивчення цієї теми, звернувшись до статті рівняння прямої в просторі - рівняння двох пересічних площин. У ній дана більш детальна інформація, детально розібрані рішення характерних прикладів і завдань, а також показаний спосіб переходу до рівнянь прямої в просторі іншого виду.

Слід зазначити, що існують різні способи завдання прямої в просторі, І на практиці пряма частіше задається не двома пересічними площинами, а тих, що направляють вектором прямої і точкою, що лежить на цій прямій. У цих випадках простіше отримати канонічні і параметричні рівняння прямої в просторі. Про них поговоримо в наступних пунктах.

Параметричні рівняння прямої в просторі.

Параметричні рівняння прямої в просторі мають вигляд ,

де x 1 ,y 1 і z 1 - координати деякої точки прямої, a x , a y і a z (a x , a y і a z одночасно не рівні нулю) - відповідні координати направляючого вектора прямої, А - деякий параметр, який може приймати будь-які дійсні значення.

При будь-якому значенні параметра по параметричних рівнянь прямої в просторі ми можемо обчислити трійку чисел,

вона буде відповідати певній точці прямої (звідси і назва цього виду рівнянь прямої). Наприклад, при

з параметричних рівнянь прямої в просторі отримуємо координати x 1 , y 1 і z 1 : .

Як приклад розглянемо пряму, яку задають параметричні рівняння виду . Ця пряма проходить через точку, а спрямовує вектор цієї прямої має координати.

Рекомендуємо продовжити вивчення теми, звернувшись до матеріалу статті параметричні рівняння прямої в просторі. У ній показаний висновок параметричних рівнянь прямої в просторі, розібрані окремі випадки параметричних рівнянь прямої в просторі, дані графічні ілюстрації, наведені розгорнуті рішення характерних завдань і вказаний зв'язок параметричних рівнянь прямої з іншими видами рівнянь прямої.

Канонічні рівняння прямої в просторі.

Дозволивши кожне з параметричних рівнянь прямої виду щодо параметра, легко перейти до канонічним рівнянням прямої в просторі виду .

Канонічні рівняння прямої в просторі визначають пряму, що проходить через точку , А тих, що направляють вектором прямої є вектор . Наприклад, рівняння прямої в канонічному вигляді відповідають прямої, що проходить через точку простору з координатами, спрямовує вектор цієї прямої має координати.

Слід зазначити, що одне або два з чисел в канонічних рівняннях прямої можуть бути рівні нулю (всі три чіслаодновременно не можуть бути рівними нулю, так як направляючий вектор прямої не може бути нульовим). Тоді запис виду вважається формальної (так як в знаменниках однієї або двох дробів будуть нулі) і її слід розуміти як , Де.

Якщо одне з чисел в канонічних рівняннях прямої дорівнює нулю, то пряма лежить в одній з координатних площин, або в площині їй паралельної. Якщо два з чіселравни нулю, то пряма або збігається з однією з координатних осей, або паралельна їй. Наприклад пряма, відповідна канонічним рівнянням прямої в просторі виду , Лежить в площині z \u003d -2, Яка паралельна координатній площині Oxy, А координатна вісь Oy визначається канонічними рівняннями.

Графічні ілюстрації цих випадків, висновок канонічних рівнянь прямої в просторі, докладні рішення характерних прикладів і завдань, а також перехід від канонічних рівнянь прямої до інших рівнянь прямої в просторі дивіться в статті канонічні рівняння прямої в просторі.

Загальне рівняння прямої. Перехід від загального до канонічного рівняння.