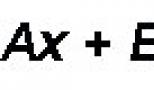Скласти рівняння площини а 2.1.2. Рівняння площини, що проходить через три точки. Вид рівняння у відрізках

Нехай точки M 1, M 2, M 3 чи не лежать на одній прямій. Як відомо, три такі точки однозначно визначають деяку площину р (рис. 199).

Виведемо рівняння площини р. Нехай М - довільна точка простору. Очевидно, що точка М належить площини ртоді і тільки тоді, коли вектори

\\ (\\ Overrightarrow (M_ (1) M) \\), \\ (\\ overrightarrow (M_ (1) M_2) \\), \\ (\\ overrightarrow (M_ (1) M_3) \\) компланарність. Необхідною і достатньою умовою компланарності трьох векторів є рівність нулю їх мішаного добутку (§ 23 *, теорема 2). Тому рівняння площини, що проходить через три точки, що не лежать на одній прямій, може бути записане таким чином:

(\\ (\\ Overrightarrow (M_ (1) M) \\), \\ (\\ overrightarrow (M_ (1) M_2) \\), \\ (\\ overrightarrow (M_ (1) M_3) \\)) \u003d 0. (1)

Якщо точки M 1, M 2 і M 3 задані координатами в деякій прямокутній декартовій системі координат, то рівняння (1) можна записати в координатах.

Нехай M 1 ( x 1 ; y 1 ; z 1), M 2 ( х 2 ; у 2 ; z 2), M 3 ( х 3 ; у 3 ; z 3) - дані точки. Позначимо координати довільної точки М площині р через х, у і z. Знайдемо координати векторів, що входять в рівняння (1):

\\ (\\ Overrightarrow (M_ (1) M) \\) \u003d ( х - х 1 ; у - у 1 ; z - z 1),

\\ (\\ Overrightarrow (M_ (1) M_2) \\) \u003d ( x 2 - x 1 ; y 2 - y 1 ; z 2 - z 1),

\\ (\\ Overrightarrow (M_ (1) M_3) \\) \u003d ( x 3 - x 1 ; у 3 - y 1 ; z 3 - z 1).

Змішане твір трьох векторів дорівнює визначнику третього порядку, в рядках якого стоять координати векторів. Отже, рівняння (1) в координатах має вигляд

$$ \\ begin (vmatrix) x-x_1 & y-y_1 & z-z_1 \\\\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\\\ x_3-x_1 & y_3-y_1 & z_3-z_1 \\ end (vmatrix) \u003d 0 \\; \\; (2) $$

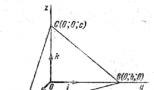
Знайдемо рівняння площини, що проходить через три точки А ( а; 0; 0), В (0; b; 0), С (0; 0; з), в яких а =/= 0, b =/= 0, c \u003d / \u003d 0. Ці точки лежать на осях координат (рис. 200).

Вважаючи в рівнянні (2) x 1 = а, у 1 = 0, z 1 = 0, x 2 = 0, у 2 = b, z 2 = 0, x 3 = 0, у 3 = 0, z 3 = з, отримаємо

$$ \\ begin (vmatrix) x-a & y & z \\\\ -a & b & 0 \\\\ -a & 0 & c \\ end (vmatrix) \u003d 0 $$

Розклавши визначник за елементами першого рядка, отримаємо рівняння

bc(х - a) + acy + abz = 0

bcx + асу + abz \u003d abc,

x / a + y / b + z / c = 1. (3)

Рівняння (3) називається рівнянням площини у відрізках, Так як числа a, b і з вказують, які відрізки відсікає площина на осях координат.

Завдання. Написати рівняння площини, що проходить через точки M 1 (-1; 4; -1), M 2 (-13; 2; -10), M 3 (6, 0, 12). Спростити отримане рівняння. Отримати рівняння даної площини в відрізках.

Рівняння (2) в даному випадку записується в такий спосіб:

$$ \\ begin (vmatrix) x + 1 & y-4 & z + 1 \\\\ -12 & -2 & -9 \\\\ 7 & -4 & 13 \\ end (vmatrix) \u003d 0 $$

Це і є рівняння даної площини. Розклавши визначник по першому рядку, отримаємо

62(х+ 1) +93(y -4)+ 62 (z + 1) = 0,

2x + 3y + 2z - 12 = 0.

Розділивши почленно на 12 і перенісши вільний член рівняння в праву частину, отримаємо рівняння даної площини в відрізках

$$ \\ frac (x) (- 6) + \\ frac (y) (4) + \\ frac (z) (6) \u003d 1 $$

З рівняння видно, що дана площину відсікає на осях координат відрізки, довжини яких дорівнюють відповідно 6, 4 і 6. Вісь Охперетинається площиною в точці з негативною абсцисою, вісь Оу - в точці з позитивною ординатою, вісь Оz - в точці з позитивною аплікатой.

1. Знайти рівняння площини, що проходить через дану точку паралельно двом даним (неколінеарна) векторах

вказівка: 1способ . Візьмемо довільну точку площини M (x, y, z). Вектори будуть компланарність, так як вони розташовані в паралельних площинах. Отже, їх змішане твір
Записуючи це умова в координатах, отримаємо рівняння шуканої площини:

Обчислювати цей визначник зручніше розкладанням по першому рядку.

2 спосіб . вектори
паралельні шуканої площини. Отже, вектор, рівний векторному добутку векторів
перпендикулярний цій площині , Тобто
і
. вектор є нормальним вектором площини . якщо
і
, То вектор знаходиться за формулою:

рівняння площини знаходимо по точці
і нормальному вектору

2. Знайти рівняння площини, що проходить через дві дані точки паралельно даному вектору
.(
неколінеарна).

вказівка: 1 спосіб. Нехай M (x, y, z) - довільна точка площини. Тоді вектори і
розташовуються в паралельних плоскостяхі, отже, компланарність, тобто їх змішане твір
Записавши цю умову в координатах, отримаємо рівняння шуканої площини .

2 спосіб . Вектор нормалі до шуканої площини буде дорівнює векторному добутку векторів
, Тобто
або в координатах:

Рівняння шуканої площини знайдеться по нормальному вектору і точці
(Або точці
) За формулою (2.1.1)

(Див. Приклад 1 пункт 2.2).

3. Знайти рівняння площини, що проходить через точку
паралельно площині 2x - 6y - 3z +5 \u003d 0.

вказівка: нормальний вектор знайдемо із загального рівняння даної площини 2x - 6y - 3z +5 \u003d 0 (2.2.1).
вектор перпендикулярний цій площині, отже, він перпендикулярний будь-якій площині, паралельної їй. вектор можна взяти за нормальний вектор шуканої площини. Складемо рівняння шуканої площини по точці
і нормальному вектору
(Див. Приклад 1 пункт 2.2).

відповідь:

4. Скласти рівняння площини, що проходить через точку
перпендикулярно лінії перетину площин 2x + y - 2z + 1 \u003d 0 і

x + y + z - 5 \u003d 0.

вказівка: 1 спосіб. Перпендикулярні кожен своїй площині вектори (координати векторів знайдені із загальних рівнянь площин, формула (2.2.1)) перпендикулярні лінії їх перетину і, отже, паралельні шуканої площини. Шукана площина проходить через точку
паралельно двох векторах
(Див. Задачу 1 пункт 5).

Рівняння шуканої площини має вигляд:

Розкриваючи визначник третього порядку по першому рядку, отримаємо шукане рівняння.

2 спосіб. Складемо рівняння площини по точці
і нормальному вектору за формулою (2.2.1). нормальний вектор дорівнює векторному добутку векторів
, Тобто.
Так як вектори
перпендикулярні лінії перетину площин, то вектор паралельний лінії перетину площин і перпендикулярний шуканої площини.

Вектори (див. Формулу 2.2.1), тоді

Складемо рівняння площини по точці
і нормальному вектору

(Див. Приклад 1 пункт 2.2)

відповідь:

5. Знайти рівняння площини, що проходить через точки
і
перпендикулярно площині 3x - y + 3z +15 \u003d 0.

вказівка: 1 спосіб. Випишемо координати нормального вектора даної п лоскості

3x - y + 3z +15 \u003d 0:
Так як площині перпендикулярні, то вектор паралельний шуканої площини Складемо рівняння шуканої площини
яка паралельна вектору і проходить через точки
(Див. Рішення задачі 2 пункт 5; 1 спосіб).

Обчислюючи визначник, отримаємо рівняння шуканої площини

10x + 15y - 5z - 70 \u003d 0
2x + 3y - z - 14 \u003d 0.

2 спосіб. Складемо рівняння шуканої площини по точці
і вектору нормалі
вектор

Складаємо рівняння шуканої площини .

10 (x - 2) +15 (y - 3) - 5 (z + 1) \u003d 0;

10x + 15y - 5z - 70 \u003d 0 (див. Задачу 2 пункт 5; 2 спосіб). Розділимо обидві частини рівняння на 5.

2x + 3y - z - 14 \u003d 0.

відповідь: 2x + 3y - z - 14 \u003d 0.

6. Скласти рівняння площини, що проходить через точки

і

вказівка: Складемо рівняння площини, що проходить через три точки (див. Приклад 1, пункт 2.3, формула 2.3.1).

Розкриваючи визначник, отримаємо

відповідь:

Зауваження. Для перевірки правильності обчислення визначника рекомендується в отримане рівняння підставити координати даних точок, через які проходить площину. Має вийти тотожність; в іншому випадку в обчисленнях допущена помилка.

7. Скласти рівняння площини, що проходить через точку
паралельно плоскостіx - 4y + 5z + 1 \u003d 0.

вказівка: Із загальної рівняння даної площини
x - 4y + 5z + 1 \u003d 0 знайдемо нормальний вектор
(Формула 2.2.1). вектор перпендикулярний до шуканої площини
Складемо рівняння площини по точці
і нормальному вектору
(Див. Приклад 1; пункт 2.2):

x - 4y + 5z + 15 \u003d 0.

відповідь:x - 4y + 5z + 15 \u003d 0.

8. Скласти рівняння площини, що проходить через точку
паралельно векторах

вказівка:Див. Рішення задачі 1 пункт 5. Вирішуємо задачу одним із зазначених способів.

відповідь: x - y - z - 1 \u003d 0.

9. Скласти рівняння площини, що проходить через точку
перпендикулярно лінії перетину площин 3x - 2y - z + 1 \u003d 0 і x - y - z \u003d 0.

вказівка:Див. Рішення задачі 4 пункт 5. Вирішуємо задачу одним із зазначених способів.

відповідь: x + 2y - z - 8 \u003d 0.

10. Знайти рівняння площини, що проходить через точки

перпендикулярно площині 3x - y - 4z \u003d 0.

вказівка:Див. Рішення задачі 5 пункт 5.

відповідь: 9x - y + 7z - 40 \u003d 0.

11. Знайти рівняння площини, що проходить через точки

паралельно прямий, обумовленою точками A (5; -2; 3) і B (6; 1; 0).

вказівка: Шукана площина паралельна прямій AB, отже, вона паралельна вектору
Рівняння шуканої площини знаходимо, як в завданні 2 пункту 5 (одним із способів).

відповідь: 3x - 4y - 3z +4 \u003d 0.

12. ТочкаP (2; -1; -2) служить підставою перпендикуляра, опущеного з початку координат на площину. Скласти рівняння цієї площини.

вказівка: нормальним вектором до шуканої площини є вектор
Знайдемо його коордінати.P (2; -1; -2) і O (0; 0; 0)

тобто
Складемо рівняння площини по точці і нормальному вектору
(Див. Приклад 1, пункт 2.2).

відповідь: 2x - y - 2z - 9 \u003d 0.

13. Скласти рівняння площини, що проходить через точку
паралельно площині: а) xoy; б) yoz; в) xoz.

вказівка: вектор
- одиничний вектор осіoz перпендикулярний площині xoy, отже, він перпендикулярний шуканої площини
Складаємо рівняння площини по точкеA (0; -1; 2) і

\u003d (0; 0; 1), тому що
(Див. Рішення задачі 3, пункт 5).
z - 2 \u003d 0.

Аналогічно вирішуємо завдання б) і в).

б)
де
(1; 0; 0).

в)
де (0; 1; 0).

y + 1 \u003d 0.

відповідь: а) z - 2 \u003d 0; б) x \u003d 0; в) y + 1 \u003d 0.

14. Скласти рівняння площини, що проходить через точки
і

B (2; 1; -1) перпендикулярно площині: а) xoy; б) xoz.

вказівка: Нормальним вектором площини xoy є вектор

\u003d (0; 0; 1) - одиничний вектор осі oz. Складемо рівняння площини, що проходить через дві точки
і B (2; 1; -1) і перпендикулярній площині, що має нормальний вектор
(0; 0; 1), використовуючи один із способів вирішення завдання 5 пункту 5.
y - 1 \u003d 0.

Аналогічно для завдання б):
де \u003d (0; 1; 0).

відповідь: а) y - 1 \u003d 0; б) x + z - 1 \u003d 0.

15. Скласти рівняння площини, що проходить через точки
і

B (2; 3; -1) паралельно осі oz.

вказівка: На осі oz можна взяти одиничний вектор \u003d (0; 0; 1). Рішення завдання аналогічно рішенню завдання 2 пункт 5 (будь-яким способом).

відповідь: x - y + 1 \u003d 0.

16. Скласти рівняння площини, що проходить через вісь ox і точку

вказівка:площина
проходить через осьox, отже, і через точку O (0; 0; 0). На осі ox можна взяти одиничний вектор \u003d (1, 0, 0). Рівняння шуканої площини складаємо по двом точкамA (2; -1; 6) і O (0; 0; 0) і вектору паралельного площині. (Див. Рішення задачі 2 пункт 5).

відповідь: 6y + z \u003d 0.

17. При якому значенні А площині Ax + 2y - 7z - 1 \u003d 0 і 2x - y + 2z \u003d 0 будуть перпендикулярні?

вказівка:Із загальних рівнянь площин

Ax + 2y - 7z - 1 \u003d 0 і
2x - y + 2z \u003d 0 вектори нормалей

\u003d (А; 2; -7) і
\u003d (2; -1; 2) (2.2.1). Умова перпендикулярності двох площин (2.6.1).

відповідь:A \u003d 8.

18. При якому значенні А площині 2x + 3y - 6z - 23 \u003d 0 і

4x + Ay - 12z + 7 \u003d 0 будуть паралельні?

вказівка:
2x + 3y - 6z - 23 \u003d 0 і
4x + Ay - 12y + 7 \u003d 0

\u003d (2; 3; -6) і
\u003d (4; A; -12) (2.2.1). Оскільки
(2.5.1)

відповідь: A \u003d 6.

19. Знайти кут між двома площинами 2x + y + z + 7 \u003d 0 і x - 2y + 3z \u003d 0.

вказівка:
2x + y + z + 7 \u003d 0 і
x - 2y + 3z \u003d 0

\u003d (2; 1; 1) і
= (1; –2; 3)

(2.4.1)

відповідь:

20. Скласти канонічні рівняння прямої, що проходить через точку

A (1; 2; -3) паралельно вектору =(1; –2; 1).

вказівка: Див. Рішення прикладу пункту 3.1.

відповідь:

21. Скласти параметричні рівняння прямої, що проходить через точку

A (-2; 3; 1) паралельно вектору =(3; –1; 2).

вказівка: Див. Рішення прикладу пункту 3.2.

відповідь:
.

22. Скласти канонічні і параметричні рівняння прямої, що проходить через точки A (1; 0; -2) і B (1; 2; -4).

вказівка: Див. Рішення прикладу 1 пункту 3.3.

відповідь:а)
б)

23. Скласти канонічні і параметричні рівняння прямої, заданої як перетин двох площин x - 2y + 3z - 4 \u003d 0 і 3x + 2y - 5z - 4 \u003d 0.

вказівка: Див. Приклад 1 пункт 3.4. Нехай z \u003d 0, тоді координати x і y точки
знаходимо з вирішення системи

Отже, точка
, Що лежить на шуканої прямий, має координати

(2; -1; 0). Для знаходження направляючого вектора шуканої прямої із загальних рівнянь площин
x - 2y + 3z - 4 \u003d 0 і
3x + 2y - 5z - 4 \u003d 0

знаходимо нормальні вектори \u003d (1; -2; 3) і
=(3; 2; –5).

Канонічні рівняння прямої знаходимо по точці
(2; -1; 0) і направля-ющему вектору

(Див. Формулу (3.1.1)).

Параметричні рівняння прямої можна знайти за формулою (3.2.1) або з канонічних рівнянь:
маємо:

відповідь:
;
.

24. Через точку
(2; -3; -4) провести пряму, паралельну прямій

.

вказівка: Канонічні рівняння шуканої прямий знайдемо по точці
і направляючої вектору Так як
то за спрямовує вектор прямий можна взяти спрямовує вектор прямойL. Далі см. Рішення задачі 23 пункт 5 або приклад 1 пункт 3.4.

відповідь:

25. Дано вершини трикутника A (-5; 7; 1), B (2; 4; -1) і C (-1; 3; 5). Знайти рівняння медіани трикутника ABC, проведеної з вершини B.

вказівка: Координати точки M знайдемо з умови AM \u003d MC (BM - медіана трикутника ABC).

З залишимо канонічні рівняння прямойBM по двох точках B (2; 4; -1) і
(Див. Приклад 1 пункт 3.3).

відповідь:

26. Скласти канонічні і параметричні рівняння прямої, що проходить через точку
(-1; -2; 2) паралельно осіox.

вказівка: вектор
- одиничний вектор осіox паралельний шуканої прямої. Отже, його можна прийняти за направляючий вектор прямої
\u003d (1, 0, 0). Складемо рівняння прямої по точці

(-1; -2: 2) і вектору \u003d (1, 0, 0) (див. Приклад пункт 3.1 і приклад 1 пункт 3.2).

відповідь:
;

27. Скласти канонічні рівняння прямої, що проходить через точку
(3; -2; 4) перпендикулярно площині 5x + 3y - 7z + 1 \u003d 0.

вказівка: Із загальної рівняння площини
5x + 3y - 7z + 1 \u003d 0 знайдемо нормальний вектор \u003d (5; 3; -7). За умовою шукана пряма
отже, вектор
тобто вектор є напрямних вектором прямойL: \u003d (5; 3; -7). Складаємо канонічні рівняння прямої по точці
(3; -2; 4) і направляючої вектору

\u003d (5; 3; -7). (Див. Приклад пункт 3.1).

відповідь:

28. Скласти параметричні рівняння перпендикуляра, опущеного з початку координат на площину 4x - y + 2z - 3 \u003d 0.

вказівка:Складемо рівняння шуканого перпендикуляра, тобто прямий, перпендикулярної площині
4x - y + 2z - 3 \u003d 0 і проходить через точку O (0; 0; 0). (Див. Рішення задачі 27 пункт 5 і прикладу 1 пункт 3.2).

відповідь:

29. Знайти точку перетину прямої
і площини

x - 2y + z - 15 \u003d 0.

вказівка: Щоб знайти точку M перетину прямої

L:
і площини

x - 2y + z - 15 \u003d 0, треба вирішити систему рівнянь:

;

Для вирішення системи канонічні рівняння прямої перетворимо до параметричних рівнянь. (Див. Задачу 23 пункт 5).

відповідь:

30. Знайти проекцію точки M (4; -3; 1) на площину x + 2y - z - 3 \u003d 0.

вказівка: Проекцією точки М на площину буде точка P - точка п ересеченія перпендикуляра, опущеного з точки М на площину
і пло-кістки Складемо параметричні рівняння пер-пендікуляра МР. (Див. Рішення задачі 28 пункт 5).

Знайдемо точку Р - точку перетину прямої МР і площини (Див. Рішення задачі 29 пункт 5).

відповідь:

31. Знайти проекцію точки А (1; 2; 1) на пряму

вказівка:Проекцією точки А на пряму L:
є т очки перетину прямої L і площини
яка проходить через точку А і перпендикулярна прямойL. З канонічних рівнянь прямої L випишемо спрямовує вектор \u003d (3; -1; 2). площина перпендикулярна прямойL, отже,
Таким чином, вектор можна взяти за нормальний вектор площини
\u003d (3; -1; 2). Складемо рівняння площини по точці А (1; 2; 1) і \u003d (3; -1; 2) (див. Приклад 1 пункт 2.2):
3 (x - 1) - 1 (y - 2) + 2 (z - 1) \u003d 0

3x - y + 2z - 3 \u003d 0. Знайдемо точку В перетину прямої і площини (див. Задачу 29 пункт 5):

відповідь:

32. Через точку M (3; -1; 0) провести пряму, паралельну двох площинах x - y + z - 3 \u003d 0 і x + y + 2z - 3 \u003d 0.

вказівка: площині
x - y + z - 3 \u003d 0 і
x + y + 2z - 3 \u003d 0 не паралельні, тому що не виконується умова (2.5.1):
площині
перетинаються. Шукана прямаяL, паралельна площинам
паралельна лінії перетину цих площин. (Див. Рішення задач 24 і 23 пункт 5).

відповідь:

33. Скласти рівняння площини, що проходить через дві прямі

вказівка:1 спосіб. Складемо рівняння шуканої площини по точці
, Що лежить на прямій , І нормальному вектору . вектор буде дорівнює векторному добутку напрямних векторів прямих
, Які знайдемо з канонічних рівнянь прямих
(Формула 3.1.1): \u003d (7; 3; 5) і

= (5; 5; –3)

координати точки
знайдемо з канонічних рівнянь прямої

Складаємо рівняння площини по точці
і вектору нормалі \u003d (- 34; 46; 20) (див. Приклад 1 пункт 2.2)
17x - 23y - 10z + 36 \u003d 0.

2 спосіб. Знаходимо напрямні вектори \u003d (7; 3; 5) і \u003d (5; 5; -3) з канонічних рівнянь прямих
крапку
(0; 2; -1) знаходимо з рівняння

. Візьмемо довільну точку площини

M (x; y; z). вектори
- компланарність, отже,
З цієї умови отримуємо рівняння площині:

відповідь: 17x - 23y - 10z +36 \u003d 0.

34. Скласти рівняння площини, що проходить через точку
(2; 0; 1) і пряму

вказівка: Переконаємося перш за все, що точка
на даній прямій не л ежит:
крапку
і спрямовує вектор знаходимо з канонічних рівнянь прямої
:
(1; -1; -1) і

\u003d (1; 2; -1). Нормальний вектор шуканої площини
Координати нормального вектора знайдемо, знаючи координати \u003d (1; 2; -1) і

= (1; 1; 2):

Складаємо рівняння площини по точці
(2; 0; 1) і нормальному вектору = (–5; 3; 1):

-5 (x - 2) + 3 (y - 0) + 1 (z - 1) \u003d 0.

відповідь: 5x - 3y - z - 9 \u003d 0.

Рівняння площини. Як скласти рівняння площини?
Взаємне розташування площин. завдання

Просторова геометрія не набагато складніше «плоскою» геометрії, і наші польоти в просторі починаються з даної статті. Для засвоєння теми необхідно добре розібратися в векторах, Крім того, бажано бути знайомим з геометрією площині - буде багато схожого, багато аналогій, тому інформація перетравиться значно краще. У серії моїх уроків 2D-світ відкривається статтею Рівняння прямої на площині. Але зараз Бетмен зійшов з плоского екрану телевізора і стартує з космодрому Байконур.

Почнемо з креслень і позначень. Схематично площину можна намалювати у вигляді паралелограма, що створює враження простору:

Площина нескінченна, але у нас є можливість зобразити лише її шматочок. На практиці крім паралелограма також прорисовують овал або навіть хмарка. Мені з технічних причин зручніше зображати площину саме так і саме в такому положенні. Реальні площині, які ми розглянемо в практичних прикладах, можуть розташовуватися як завгодно - подумки візьміть креслення в руки і покрутіть його в просторі, надавши площині будь-який нахил, будь-який кут.

позначення: Площині прийнято позначати маленькими грецькими буквами, мабуть, щоб не плутати їх з прямий на площині або з прямої в просторі. Я звик використовувати букву. На кресленні саме буква «сигма», а зовсім не дірочка. Хоча, дірява площину, це, безумовно, дуже забавно.

У ряді випадків для позначення площин зручно використовувати ті ж грецькі літери з нижніми підрядковими індексами, наприклад,.

Очевидно, що площина однозначно визначається трьома різними точками, що не лежать на одній прямій. Тому досить популярні трьохбуквені позначення площин - за належними їм точкам, наприклад, і т.д. Нерідко букви беруть у круглі дужки:, щоб не переплутати площину з іншого геометричною фігурою.

Для досвідчених читачів наведу меню швидкого доступу:

• Як скласти рівняння площини по точці і двох векторах?
• Як скласти рівняння площини по точці і вектору нормалі?

і ми не будемо нудитися довгими очікуваннями:

Загальне рівняння площини

Загальне рівняння площини має вигляд, де коефіцієнти одночасно не рівні нулю.

Ряд теоретичних викладок і практичних завдань справедливі як для звичного ортонормированного базису, так і для афінного базису простору (якщо масло - масляне, поверніться до уроку Лінійна (не) залежність векторів. базис векторів). Для простоти будемо вважати, що всі події відбуваються в ортонормированном базисі і декартовій прямокутній системі координат.

А тепер трохи потренуємо просторову уяву. Нічого страшного, якщо у вас воно погане, зараз трохи розвинемо. Навіть для гри на нервах потрібні тренування.

У найзагальнішому випадку, коли числа не рівні нулю, площина перетинає всі три координатні осі. Наприклад, так:

Ще раз повторю, що площину нескінченно триває на всі боки, і у нас є можливість зобразити тільки її частину.

Розглянемо найпростіші рівняння площин:

Як розуміти дане рівняння? Вдумайтеся: «зет» ЗАВЖДИ, при будь-яких значеннях «ікс» і «ігрек» дорівнює нулю. Це рівняння «рідний» координатної площини. Дійсно, формально рівняння можна переписати так: , Звідки добре видно, що нам по барабану, які значення приймають «ікс» і «ігрек», важливо, що «зет» дорівнює нулю.

аналогічно:
- рівняння координатної площини;
- рівняння координатної площини.

Трохи ускладнити завдання, розглянемо площину (тут і далі в параграфі припускаємо, що числові коефіцієнти не рівні нулю). Перепишемо рівняння у вигляді:. Як його розуміти? «Ікс» ЗАВЖДИ, при будь-яких значеннях «ігрек» та «зет» дорівнює деякому числу. Ця площина паралельна координатній площині. Наприклад, площина паралельна площині і проходить через точку.

аналогічно:
- рівняння площини, яка паралельна координатній площині;
- рівняння площини, яка паралельна координатній площині.

Додамо членів:. Рівняння можна переписати так:, тобто «зет» може бути будь-яким. Що це означає? «Ікс» і «ігрек» пов'язані співвідношенням, яке прокреслює в площині деяку пряму (впізнаєте рівняння прямої на площині?). Оскільки «зет» може бути будь-яким, то ця пряма «тиражується» на будь-якій висоті. Таким чином, рівняння визначає площину, паралельну координатної осі

аналогічно:
- рівняння площини, яка паралельна координатної осі;
- рівняння площини, яка паралельна координатної осі.

Якщо вільні члени нульові, то площини будуть безпосередньо проходити через відповідні осі. Наприклад, класична «пряма пропорційність»:. Накресліть в площині пряму і подумки розмножте її вгору і вниз (так як «зет» any). Висновок: площину, задана рівнянням, проходить через координатну вісь.

Завершуємо огляд: рівняння площини проходить через початок координат. Ну, тут абсолютно очевидно, що точка задовольняє даному рівнянню.

І, нарешті, випадок, який зображений на кресленні: - площину дружить з усіма координатними осями, при цьому вона завжди «відсікає» трикутник, який може розташовуватися в будь-якому з восьми октантів.

Лінійні нерівності в просторі

Для розуміння інформації необхідно добре вивчити лінійні нерівності на площині, Оскільки багато речей буду схожі. Параграф носитиме короткий оглядовий характер з декількома прикладами, так як матеріал на практиці зустрічається досить рідко.

Якщо рівняння задає площину, то нерівності
задають півпростору. Якщо нерівність Нечитка (два останніх у списку), то в рішення нерівності крім полупространства входить і сама площина.

приклад 5

Знайти одиничний нормальний вектор площини .

Рішення: Єдиний вектор - це вектор, довжина якого дорівнює одиниці. Позначимо цей вектор через. Цілком зрозуміло, що вектори колінеарні:

Спочатку з рівняння площині знімемо вектор нормалі:.

Як знайти одиничний вектор? Для того щоб знайти одиничний вектор, потрібно кожну координату вектора розділити на довжину вектора.

Перепишемо вектор нормалі в вигляді і знайдемо його довжину:

Відповідно до вищесказаного:

відповідь:

Перевірка:, що і було потрібно перевірити.

Читачі, які уважно вивчили останній параграф уроку, напевно, помітили, що координати одиничного вектора - це в точності напрямні косинуси вектора:

Відвернемося від розібраної завдання: коли вам дано довільний ненульовий вектор, І за умовою потрібно знайти його напрямні косинуси (див. Останні завдання уроку Скалярний добуток векторів), То ви, по суті, знаходите і одиничний вектор, колінеарний даному. Фактично два завдання в одному флаконі.

Необхідність знайти одиничний вектор нормалі виникає в деяких задачах математичного аналізу.

З Вивуджування нормального вектора розібралися, тепер відповімо на протилежний питання:

Як скласти рівняння площини по точці і вектору нормалі?

Цю жорстку конструкцію вектора нормалі і точки добре знає мету для гри в дартс. Будь ласка, витягніть руку вперед і подумки виберіть довільну точку простору, наприклад, маленьку кішечку в серванті. Очевидно, що через дану точку можна провести єдину площину, перпендикулярну вашій руці.

Рівняння площини, що проходить через точку перпендикулярно вектору, виражається формулою:

Можна задавати різними способами (однією точкою і вектором, двома точками і вектором, трьома крапками і ін.). Саме з огляду на це рівняння площині може мати різні види. Також при дотриманні певних умов площині можуть бути паралельними, перпендикулярними, пересічними і т.д. Про це і поговоримо в даній статті. Ми навчимося складати загальне рівняння площини і не тільки.

Нормальний вид рівняння

Припустимо, є простір R 3, яке має прямокутну координатну систему XYZ. Задамо вектор α, який буде випущений з початкової точки О. Через кінець вектора α проведемо площину П, яка буде йому перпендикулярна.

Позначимо на П довільну точку Q \u003d (х, у, z). Радіус-вектор точки Q підпишемо буквою р. При цьому довжина вектора α дорівнює р \u003d IαI і Ʋ \u003d (cosα, cosβ, cosγ).

Це одиничний вектор, який направлений в сторону, як і вектор α. α, β і γ - це кути, які утворюються між вектором Ʋ і позитивними напрямками осей простору х, у, z відповідно. Проекція будь-якої точки QεП на вектор Ʋ є постійною величиною, яка дорівнює р: (р, Ʋ) \u003d р (р≥0).

Зазначене рівняння має сенс, коли р \u003d 0. Єдине, площину П в цьому випадку буде перетинати точку О (α \u003d 0), яка є початком координат, і одиничний вектор Ʋ, випущений з точки О, буде перпендикулярний до П, незважаючи на його напрямок, що означає, що вектор Ʋ визначається з точністю до знака. Попереднє рівняння є рівнянням нашої площині П, вираженим у векторній формі. А ось в координатах його вид буде таким:

Р тут більше або дорівнює 0. Ми знайшли рівняння площини в просторі в нормальному вигляді.

загальне рівняння

Якщо рівняння в координатах помножимо на будь-яке число, яке не дорівнює нулю, отримаємо рівняння, еквівалентне даному, що визначає ту саму площину. Воно буде мати такий вигляд:

Тут А, В, С - це числа, одночасно відмінні від нуля. Це рівняння називається як рівняння площини загального вигляду.

Рівняння площин. окремі випадки

Рівняння в загальному вигляді може видозмінюватися при наявності додаткових умов. Розглянемо деякі з них.

Припустимо, що коефіцієнт А дорівнює 0. Це означає, що дана площину паралельна заданій осі Ох. У цьому випадку вид рівняння зміниться: Ву + Cz + D \u003d 0.

Аналогічно вид рівняння буде змінюватися і за таких умов:

• По-перше, якщо В \u003d 0, то рівняння зміниться на Ах + Cz + D \u003d 0, що свідчитиме про паралельність до осі Оу.
• По-друге, якщо С \u003d 0, то рівняння перетворюється в Ах + Ву + D \u003d 0, що буде говорити про паралельність до заданої осі Oz.
• По-третє, якщо D \u003d 0, рівняння буде виглядати як Ах + Ву + Cz \u003d 0, що буде означати, що площина перетинає О (початок координат).
• По-четверте, якщо A \u003d B \u003d 0, то рівняння зміниться на Cz + D \u003d 0, що буде доводити паралельність до Oxy.
• По-п'яте, якщо B \u003d C \u003d 0, то рівняння стане Ах + D \u003d 0, а це означає, що площина до Oyz паралельна.
• По-шосте, якщо A \u003d C \u003d 0, то рівняння набуде вигляду Ву + D \u003d 0, тобто буде повідомляти про паралельність до Oxz.

Вид рівняння у відрізках

У разі коли числа А, В, С, D відмінні від нуля, вид рівняння (0) може бути наступним:

х / а + у / b + z / с \u003d 1,

в якому а \u003d -D / А, b \u003d -D / В, з \u003d -D / С.

Отримуємо в результаті Варто відзначити, що дана площину буде перетинати вісь Ох у точці з координатами (а, 0,0), Оу - (0, b, 0), а Oz - (0,0, с).

З урахуванням рівняння х / а + у / b + z / с \u003d 1 неважко візуально уявити розміщення площині щодо заданої координатної системи.

Координати нормального вектора

Нормальний вектор n до площини П має координати, які є коефіцієнтами загального рівняння даної площини, тобто n (А, В, С).

Для того щоб визначити координати нормалі n, досить знати загальне рівняння заданої площині.

При використанні рівняння у відрізках, яке має вигляд х / а + у / b + z / с \u003d 1, як і при використанні загального рівняння, можна записати координати будь-якого нормального вектора заданої площині: (1 / а + 1 / b + 1 / с).

Варто відзначити, що нормальний вектор допомагає вирішити різноманітні завдання. До найпоширеніших належать завдання, які полягають в доказі перпендикулярності або паралельності площин, завдання по знаходженню кутів між площинами або кутів між площинами і прямими.

Вид рівняння площини згідно координатам точки і нормального вектора

Ненульовий вектор n, перпендикулярний заданій площині, називають нормальним (нормаллю) для заданої площині.

Припустимо, що в координатному просторі (прямокутної системі координат) Oxyz задані:

• точка Мₒ з координатами (хₒ, уₒ, zₒ);
• нульовий вектор n \u003d А * i + В * j + С * k.

Потрібно скласти рівняння площини, яка буде проходити через точку Мₒ перпендикулярно нормалі n.

У просторі виберемо будь-яку довільну точку і позначимо її М (х у, z). Нехай радіус-вектор будь-якої точки М (х, у, z) буде r \u003d х * i + у * j + z * k, а радіус-вектор точки Мₒ (хₒ, уₒ, zₒ) - rₒ \u003d хₒ * i + уₒ * j + zₒ * k. Точка М буде належати заданої площині, якщо вектор МₒМ буде перпендикулярний вектору n. Запишемо умову ортогональності за допомогою скалярного твори:

[МₒМ, n] \u003d 0.

Оскільки МₒМ \u003d r-rₒ, векторне рівняння площини виглядати буде так:

Дане рівняння може мати й іншу форму. Для цього використовуються властивості скалярного твори, а перетворюється ліва сторона рівняння. \u003d -. Якщо позначити як з, то вийде наступне рівняння: - з \u003d 0 або \u003d с, яке виражає сталість проекцій на нормальний вектор радіус-векторів заданих точок, які належать площині.

Тепер можна отримати координатний вид запису векторного рівняння нашої площині \u003d 0. Оскільки r-rₒ \u003d (х-хₒ) * i + (у-уₒ) * j + (z-zₒ) * k, а n \u003d А * i + В * j + С * k, ми маємо:

Виходить, у нас утворюється рівняння площини, що проходить через точку перпендикулярно нормалі n:

А * (х- хₒ) + В * (у-уₒ) С * (z-zₒ) \u003d 0.

Вид рівняння площини згідно координатам двох точок і вектора, колінеарну площині

Задамо дві довільні точки М '(х', у ', z') і М "(х", у ", z"), а також вектор а (а ', а ", а ‴).

Тепер ми зможемо скласти рівняння заданої площині, яка буде проходити через наявні точки М 'і М ", а також будь-яку точку М з координатами (х, у, z) паралельно заданому вектору а.

При цьому вектори М'М \u003d (х-х '; у-у'; zz ') і М "М \u003d (х" х'; у "-у '; z" -z') повинні бути компланарними з вектором а \u003d (а ', а ", а ‴), а це означає, що (М'М, М" М, а) \u003d 0.

Отже, наше рівняння площини в просторі буде виглядати так:

Вид рівняння площині, що перетинає три точки

Припустимо, у нас є три точки: (х ', у', z '), (х ", у", z "), (х ‴, у ‴, z ‴), які не належать одній прямій. Необхідно написати рівняння площини, що проходить через задані три точки. Теорія геометрії стверджує, що такого роду площину дійсно існує, ось тільки вона єдина і неповторна. Оскільки ця площина перетинає точку (х ', у', z '), вид її рівняння буде таким:

Тут А, В, С відмінні від нуля одночасно. Також задана площина перетинає ще дві точки: (х ", у", z ") і (х ‴, у ‴, z ‴). У зв'язку з цим повинні виконуватися такого роду умови:

Зараз ми можемо скласти однорідну систему з невідомими u, v, w:

У нашому випадку х, у або z виступає довільної точкою, яка задовольняє рівняння (1). З огляду на рівняння (1) і систему з рівнянь (2) і (3), системі рівнянь, зазначеної на малюнку вище, задовольняє вектор N (А, В, С), який є нетривіальним. Саме тому визначник даної системи дорівнює нулю.

Рівняння (1), яке у нас вийшло, це і є рівняння площині. Через 3 точки вона точно проходить, і це легко перевірити. Для цього потрібно розкласти наш визначник за елементами, що знаходяться в першому рядку. З існуючих властивостей визначника випливає, що наша площину одночасно перетинає три спочатку задані точки (х ', у', z '), (х ", у", z "), (х ‴, у ‴, z ‴). Тобто ми вирішили поставлене перед нами завдання.

Двухгранний кут між площинами

Двухгранний кут є просторовою геометричну фігуру, утворену двома півплощини, які виходять з однієї прямої. Іншими словами, це частина простору, яка обмежується даними напівплощиною.

Припустимо, у нас є дві площини з наступними рівняннями:

Нам відомо, що вектори N \u003d (А, В, С) і N¹ \u003d (А¹, В¹, С¹) перпендикулярні згідно із заданими площинах. У зв'язку з цим кут φ між векторами N і N¹ дорівнює розі (двухгранний), який знаходиться між цими площинами. Скалярний твір має вигляд:

NN¹ \u003d | N || N¹ | cos φ,

саме тому

cosφ \u003d NN¹ / | N || N¹ | \u003d (АА¹ + ВВ¹ + СС¹) / ((√ (А ² + В² + с?)) * (√ (А¹) ² + (В¹) ² + (С¹) ²)).

Досить врахувати, що 0≤φ≤π.

Насправді дві площини, які перетинаються, утворюють два кута (двухгранних): φ 1 і φ 2. Сума їх дорівнює π (φ 1 + φ 2 \u003d π). Що стосується їх косинусів, то їх абсолютні величини рівні, але розрізняються вони знаками, тобто cos φ 1 \u003d -cos φ 2. Якщо в рівнянні (0) замінити А, В і С на числа -А, -В і -С відповідно, то рівняння, яке ми отримаємо, буде визначати цю ж площину, єдине, кут φ в рівнянні cos φ \u003d NN 1 / | N || N 1 | буде замінений на π-φ.

Рівняння перпендикулярній площині

Перпендикулярними називаються площині, між якими кут дорівнює 90 градусів. Використовуючи матеріал, викладений вище, ми можемо знайти рівняння площини, перпендикулярної інший. Припустимо, у нас є дві площини: Ах + Ву + Cz + D \u003d 0 і А¹х + В¹у + С¹z + D \u003d 0. Ми можемо стверджувати, що перпендикулярними вони будуть, якщо cosφ \u003d 0. Це означає, що NN¹ \u003d АА¹ + ВВ¹ + СС¹ \u003d 0.

Рівняння паралельній площині

Паралельними називаються дві площини, які не містять спільних точок.

Умова (їх рівняння ті ж, що і в попередньому пункті) полягає в тому, що вектори N і N¹, які до них перпендикулярні, Колінеарні. А це значить, що виконуються наступні умови пропорційності:

А / А¹ \u003d В / В¹ \u003d С / С¹.

Якщо умови пропорційності є розширеними - А / А¹ \u003d В / В¹ \u003d С / С¹ \u003d DD¹,

це свідчить про те, що дані площини збігаються. А це означає, що рівняння Ах + Ву + Cz + D \u003d 0 і А¹х + В¹у + С¹z + D¹ \u003d 0 описують одну площину.

Відстань до площини від точки

Припустимо, у нас є площину П, яка задана рівнянням (0). Необхідно знайти до неї відстань від точки з координатами (хₒ, уₒ, zₒ) \u003d Qₒ. Щоб це зробити, потрібно привести рівняння площини П в нормальний вигляд:

(Ρ, v) \u003d р (р≥0).

В даному випадку ρ (х, у, z) є радіус-вектором нашої точки Q, розташованої на П, р - це довжина перпендикуляра П, який був випущений з нульової точки, v - це одиничний вектор, який розташований в напрямку а.

Різниця ρ-ρº радіус-вектора який-небудь точки Q \u003d (х, у, z), що належить П, а також радіус-вектора заданої точки Q 0 \u003d (хₒ, уₒ, zₒ) є таким вектором, абсолютна величина проекції якого на v дорівнює відстані d, яке потрібно знайти від Q 0 \u003d (хₒ, уₒ, zₒ) до П:

D \u003d | (ρ-ρ 0, v) |, але

(Ρ-ρ 0, v) \u003d (ρ, v) - (ρ 0, v) \u003d р- (ρ 0, v).

Ось і виходить,

d \u003d | (ρ 0, v) -р |.

Таким чином, ми знайдемо абсолютне значення отриманого виразу, тобто шукане d.

Використовуючи мову параметрів, отримуємо очевидне:

d \u003d | Ахₒ + Вуₒ + Czₒ | / √ (А ² + В² + с?).

Якщо задана точка Q 0 знаходиться по іншу сторону від площини П, як і початок координат, то між вектором ρ-ρ 0 і v знаходиться отже:

d \u003d - (ρ-ρ 0, v) \u003d (ρ 0, v) -р\u003e 0.

У разі коли точка Q 0 спільно з початком координат розташовується по одну і ту ж сторону від П, то створюваний кут гострий, тобто:

d \u003d (ρ-ρ 0, v) \u003d р - (ρ 0, v)\u003e 0.

У підсумку виходить, що в першому випадку (ρ 0, v)\u003e р, у другому (ρ 0, v)<р.

Дотична площину і її рівняння

Що стосується площину до поверхні в точці дотику мº - це площина, яка містить всі можливі дотичні до кривих, проведеним через цю точку на поверхні.

При такому вигляді рівняння поверхні F (х, у, z) \u003d 0 рівняння дотичної площини в дотичній точці мº (хº, уº, zº) буде виглядати так:

F х (хº, уº, zº) (х- хº) + F х (хº, уº, zº) (у-уº) + F х (хº, уº, zº) (z-zº) \u003d 0.

Якщо задати поверхню в явній формі z \u003d f (х, у), то дотична площину буде описана рівнянням:

z-zº \u003d f (хº, уº) (х- хº) + f (хº, уº) (у-уº).

Перетин двох площин

В розташована система координат (прямокутна) Oxyz, дано дві площини П 'і П ", які перетинаються і не збігаються. Оскільки будь-яка площина, що знаходиться в прямокутній системі координат, визначається загальним рівнянням, будемо вважати, що П 'і П "задаються рівняннями А'х + В'у + С'z + D' \u003d 0 і А" х + В "у + З "z + D" \u003d 0. У такому випадку маємо нормаль n '(А', В ', С') площині П 'і нормаль n "(А", В ", С") площині П ". Оскільки наші площині не паралельні і не збігаються, то ці вектори не є колінеарними. Використовуючи мову математики, ми цю умову можемо записати так: n '≠ n "↔ (А', В ', С') ≠ (λ * А", λ * В ", λ * С"), λεR. Нехай пряма, яка лежить на перетині П 'і П ", буде позначатися літерою а, в цьому випадку а \u003d П' ∩ П".

а - це пряма, що складається з безлічі всіх точок (загальних) площин П 'і П ". Це означає, що координати будь-якої точки, що належить прямій а, повинні одночасно задовольняти рівняння А'х + В'у + С'z + D '\u003d 0 і А "х + В" у + С "z + D" \u003d 0. Значить, координати точки будуть приватним рішенням наступної системи рівнянь:

У підсумку виходить, що рішення (загальне) цієї системи рівнянь буде визначати координати кожної з точок прямої, яка буде виступати точкою перетину П 'і П ", і визначати пряму а в системі координат Oxyz (прямокутної) в просторі.

Щоб отримати загальне рівняння площини, розберемо площину, що проходить через задану точку.

Нехай в просторі є три вже відомі нам осі координат - Ox, Oy і Oz. Потримаємо аркуш паперу так, щоб він залишався плоским. Площиною буде сам лист і його продовження у всіх напрямках.

нехай P довільна площина в просторі. Всякий перпендикулярний їй вектор називається вектором нормалі до цієї площини. Природно, мова йде про ненулевом векторі.

Якщо відома якась точка площині P і який-небудь вектор нормалі до неї, то цими двома умовами площину в просторі цілком визначена (Через задану точку можна провести єдину площину, перпендикулярну даному вектору). Загальне рівняння площини буде мати вигляд:

Отже, умови, якими задається рівняння площині, є. Щоб отримати саме рівняння площини, Що має наведений вище вид, візьмемо на площині P довільну точку M зі змінними координатами x, y, z. Ця точка належить площині тільки в тому випадку, коли вектор перпендикулярний вектору (Рис. 1). Для цього, згідно з умовою перпендикулярності векторів, необхідно і достатньо, щоб скалярний добуток цих векторів дорівнювало нулю, тобто

Вектор заданий за умовою. Координати вектора знайдемо за формулою :

.

Тепер, використовуючи формулу скалярного твори векторів , Висловимо скалярний твір в координатної формі:

Так як точка M (x; y; z) обрана на площині довільно, то останнім рівнянням задовольняють координати будь-якої точки, що лежить на площині P. для точки N, Що не лежить на заданій площині,, тобто рівність (1) порушується.

Приклад 1. Скласти рівняння площини, що проходить через точку і перпендикулярної вектору.

Рішення. Використовуємо формулу (1), ще раз подивимося на неї:

У цій формулі числа A , B і C координати вектора, а числа x0 , y0 і z0 - координати точки.

Обчислення дуже прості: підставляємо ці числа в формулу і отримуємо

Множимо все, що потрібно помножити і складаємо просто числа (які без букв). результат:

.

Необхідну рівняння площини в цьому прикладі виявилося виражено загальним рівнянням першого ступеня щодо змінних координат x, y, z довільної точки площини.

Отже, рівняння виду

називається загальним рівнянням площини .

Приклад 2.Побудувати в прямокутній декартовій системі координат площину, задану рівнянням .

Рішення. Для побудови площини необхідно і достатньо знати будь-які три її точки, що не лежать на одній прямій, наприклад, точки перетину площини з осями координат.

Як знайти ці точки? Щоб знайти точку перетину з віссю Oz , Потрібно в рівняння, дане в умові завдання, замість ікс і Ігрека підставити нулі: x = y \u003d 0. Тому отримуємо z \u003d 6. Таким чином, задана площина перетинає вісь Oz в точці A(0; 0; 6) .

Точно так же знаходимо точку перетину площини з віссю Oy . при x = z \u003d 0 отримуємо y \u003d -3, тобто точку B(0; −3; 0) .

І, нарешті, знаходимо точку перетину нашої площині з віссю Ox . при y = z \u003d 0 отримаємо x \u003d 2, тобто точку C(2; 0; 0). З трьох отриманим в нашому рішенні точкам A(0; 0; 6) , B(0; -3; 0) і C(2; 0; 0) будуємо задану площину.

Розглянемо тепер окремі випадки загального рівняння площини. Це випадки, коли ті чи інші коефіцієнти рівняння (2) звертаються в нуль.

1. При D \u003d0 рівняння визначає площину, що проходить через початок координат, так як координати точки 0 (0; 0; 0) задовольняють цьому рівнянню.

2. При A \u003d0 рівняння визначає площину, паралельну осі Ox, Оскільки вектор нормалі цій площині перпендикулярний осі Ox (Його проекція на вісь Ox дорівнює нулю). Аналогічно, при B \u003d0 площину паралельна осі Oy, А при C \u003d0 площину паралельна осі Oz.

3. При A \u003d D \u003d 0 рівняння визначає площину, що проходить через вісь Ox, Оскільки вона паралельна осі Ox (A \u003dD \u003d 0). Аналогічно, площина проходить через вісь Oy, А площину через вісь Oz.

4. При A \u003d B \u003d0 рівняння визначає площину, паралельну координатної площини xOy, Оскільки вона паралельна осях Ox (A \u003d 0) і Oy (B \u003d 0). Аналогічно, площина паралельна площині yOz, А площину - площині xOz.

5. При A \u003d B \u003d D \u003d0 рівняння (або z \u003d0) визначає координатну площину xOy, Так як вона паралельна площині xOy (A \u003d B \u003d 0) і проходить через початок координат ( D \u003d0). Аналогічно, рівняння y \u003d0 в просторі визначає координатну площину xOz, А рівняння x \u003d0 - координатну площину yOz.

Приклад 3. Скласти рівняння площини P , Що проходить через вісь Oy і точку.

Рішення. Отже, площина проходить через вісь Oy . Тому в її рівнянні y \u003d 0 і це рівняння має вигляд. Для визначення коефіцієнтів A і C скористаємося тим, що точка належить площині P .

Тому серед її координат є такі, які можна підставити в рівняння площини, яке ми вже вивели (). Дивимося ще раз на координати точки:

M0 (2; −4; 3) .

Серед них x = 2 , z \u003d 3. Підставляємо їх в рівняння загального вигляду і отримуємо рівняння для нашого окремого випадку:

2A + 3C = 0 .

Ми залишаємо 2 A в лівій частині рівняння, переносимо 3 C в праву частину і отримуємо

A = −1,5C .

Підставивши знайдене значення A в рівняння, отримаємо

або.

Це і є рівняння, необхідне в умові прикладу.

Вирішити завдання на рівняння площини самостійно, а потім подивитися рішення

Приклад 4. Визначити площину (або площини, якщо більше однієї) щодо координатних осей або координатних площин, якщо площину (площині) задана рівнянням.

Рішення типових задач, які бувають на контрольних роботах - в посібнику "Завдання на площину: паралельність, перпендикулярність, перетин трьох площин в одній точці".

Рівняння площини, що проходить через три точки

Як уже згадувалося, необхідною і достатньою умовою для побудови площини, крім однієї точки і вектора нормалі, є також три точки, що не лежать на одній прямій.

Нехай дано три різні точки, і, що не лежать на одній прямій. Оскільки вказані три точки не лежать в одній прямий, вектори і не колінеарні, а тому будь-яка точка площині лежить в одній площині з точками, і тоді і тільки тоді, коли вектори, і компланарність, тобто тоді і тільки тоді, коли мішаний добуток цих векторів дорівнює нулю.

Використовуючи вираз змішаного твори в координатах, отримаємо рівняння площини

(3)

Після розкриття визначника це рівняння стає рівнянням виду (2), тобто загальним рівнянням площини.

Приклад 5. Скласти рівняння площини, що проходить через три дані точки, що не лежать на одній прямій:

і визначити окремий випадок загального рівняння прямої, якщо такий має місце.

Рішення. За формулою (3) маємо:

Нормальне рівняння площині. Відстань від точки до площини

Нормальним рівнянням площини називається її рівняння, записане у вигляді