Як побудувати проекцію вектора на вісь. Проекції векторів на координатні осі. Проекція вектора на вісь. властивості проекцій

Основні поняття ВЕКТОРНОЇ АЛГЕБРИ

Скалярні і векторні величини

З курсу елементарної фізики відомо, що деякі фізичні величини, такі як температура, об'єм, маса тіла, щільність і т.д., визначаються тільки числовим значенням. Такі величини називаються скалярними величинами, або скалярами.

Для визначення ж деяких інших величин, таких як сила, швидкість, прискорення і тому подібних, крім числових значень необхідно задати ще і їх напрям в просторі. Величини, які крім абсолютної величини характеризуються ще й напрямком, називаються векторними.

визначення Вектором називається спрямований відрізок, який визначається двома точками: перша точка визначає початок вектора, а друга - його кінець. Тому ще говорять, що вектор - це впорядкована пара точок.

На малюнку вектор зображується відрізком прямої, на якому стрілкою зазначене напрямок від початку вектора до його кінця. Наприклад, рис. 2.1.

Якщо початок вектора збігається з точкою , А кінець з точкою , То вектор позначається
. Крім цього, часто вектори позначають однією маленькою буквою зі стрілкою над нею . У книжках іноді стрілку опускають, тоді для позначення вектора вживають жирний шрифт.

До векторах відноситься нульовий вектор, У якого початок і кінець збігаються. він позначається або просто .

Відстань між початком і кінцем вектора називається його довжиною, або модулем. Модуль вектора позначається двома вертикальними рисками ліворуч:
, Або без стрілок
або .

Вектори, паралельні до однієї прямої, називаються колінеарними.

Вектори, що лежать в одній площині або паралельні одній і тій же площині, називаються компланарними.

Нульовий вектор вважається колінеарну до будь-якого вектору. Довжина його дорівнює 0.

визначення два вектора
і
називаються рівними (рис. 2.2), якщо вони:
1)колінеарні; 2) сонаправлени 3) рівні по довжині.

Це записують так:
(2.1)

З визначення рівності векторів випливає, що при паралельному перенесенні вектора виходить вектор, рівний початкового, тому початок вектора можна розмістити в будь-яку точку простору. Такі вектори (в теоретичної механіки, геометрії), початок яких можна розміщувати в будь-якій точці простору, називають вільними. І саме такі вектори ми будемо розглядати.

визначення система векторів
називається лінійно залежною, якщо існують такі постійні
, Серед яких є хоча б одна відмінна від нуля, і для яких виконується рівність.

визначення Базисом в просторі називаються довільні три некомпланарних вектора, які взяті в певній послідовності.

визначення якщо
- базис і вектор, то числа
називаються координатами вектора в даному базисі.

Координати вектора будемо писати в фігурних дужках після позначення вектора. Так наприклад,
означає, що вектор в деякому обраному базисі має розкладання:
.

З властивостей множення вектора на число та додавання векторів випливає твердження щодо лінійних дій над векторами, які задані координатами.

Для того, щоб знайти координати вектора, якщо відомі координати його початку і кінця, необхідно з відповідною координати його кінця відняти координату початку.

Лінійні операції над векторами

Лінійними операціями над векторами називаються операції додавання (віднімання) векторів і множення вектора на число. Розглянемо їх.

визначення твором вектора на число
називається вектор, що збігається за напрямком з вектором , якщо
, Що має протилежний зміст, якщо
негативне. Довжина цього вектора дорівнює добутку довжини вектора на модуль числа
.

П ример . побудувати вектор
, якщо
і
(Рис. 2.3).

При множенні вектора на число його координати множаться на це число.

Дійсно, якщо, то

твором вектора на
називається вектор
;
- протилежний спрямований .

Відзначимо, що вектор, довжина якого дорівнює 1, називається одиничним(або ортом).

Користуючись операцією множення вектора на число, будь-який вектор можна виразити через одиничний вектор того ж напрямку. Дійсно, поділивши вектор на його довжину (Тобто помноживши на ), Отримаємо одиничний вектор того ж напрямку, що і вектор . Його будемо позначати
. Звідси слідує що
.

визначення Сумою двох векторів і називається вектор , Який виходить з їх загального початку і є діагоналлю паралелограма, сторони якого вектори і (Рис. 2.4).

.

За визначенням рівних векторів
тому
-правило трикутника. Правило трикутника можна поширити на будь-яку кількість векторів і таким чином отримати правило багатокутника:
- це вектор, який з'єднує початок першого вектора з кінцем останнього вектора (Рис. 2.5).

Отже, для того щоб побудувати вектор суми, треба до кінця першого вектора прилаштувати початок другого, до кінця другого прилаштувати початок третього і так далі. Тоді вектором суми і буде вектор, який з'єднує початок першого з векторів з кінцем останнього.

При додаванні векторів складаються і їх відповідні координати

Дійсно, якщо і
,

якщо вектори
і нЕ компланарність, то їх сума є діагоналлю
паралелепіпеда, побудованого на цих векторах (рис. 2.6)

,

де

властивості:

- коммутативность;

- асоціативність;

- дистрибутивность по відношенню до множення на число

.

Тобто векторну суму можна перетворювати за тими ж правилами, що і алгебраїчну.

визначенняРізницею двох векторів і називають такий вектор , Який при додаванні з вектором дає вектор . Тобто
якщо
. геометрично являє собою другу діагональ паралелограма, побудованого на векторах і із загальним початком і спрямовану з кінця вектора в кінець вектора (Рис. 2.7).

Проекція вектора на вісь. властивості проекцій

Згадаймо поняття числової осі. Числовою віссю називають пряму, на якій визначено:

напрямок (→);

початок відліку (точка О);

відрізок, який приймають за одиницю масштабу.

Нехай є вектор
і вісь . з точок і опустимо перпендикуляри на вісь . отримаємо точки і - проекції точок і (Рис. 2.8 а).

визначення проекцією вектора
на вісь називається довжина відрізка
цієї осі, який розташований між підставами проекцій початку і кінця вектора
на вісь . Вона береться зі знаком плюс, якщо напрямок відрізка
збігається з напрямком осі проекцій, і зі знаком мінус, якщо ці напрямки протилежні. позначення:
.

Про пределеніе Кутом між вектором
і віссю називається кут , На який необхідно найкоротшим чином повернути вісь , Щоб вона збігалася з напрямком вектора
.

знайдемо
:

На рис.2.8 а представлена:
.

На рис. 2.8 б): .

Проекція вектора на вісь дорівнює добутку довжини цього вектора на косинус кута між вектором і віссю проекцій:
.

властивості проекцій:

якщо
, То вектори називаються ортогональними

приклад . задані вектори
,
.Тоді

.

Приклад. Якщо початок вектора
знаходиться в точці
, А кінець в точці
, То вектор
має координати:

Про пределеніе Кутом між двома векторами і називається найменший кут
(Рис. 2.13) між цими векторами, зведеними в загальне початок .

Кут між векторами і символічно записують таким чином: .

З визначення випливає, що кут між векторами може змінюватися в межах
.

якщо
, То вектори називаються ортогональними.

.

Визначення. Косинуси кутів вектора з осями координат називаються напрямними косинусами вектора. якщо вектор
утворює з осями координат кути

.

Будуть і завдання для самостійного рішення, до яких можна подивитися відповіді.

поняття вектора

Перш ніж Ви дізнаєтеся все про вектори і операціях над ними, налаштуйтеся на рішення нескладного завдання. Є вектор Вашої підприємливості та вектор Ваших інноваційних здібностей. Вектор підприємливості веде Вас до Цілі 1, а вектор інноваційних здібностей - до Мети 2. Правила гри такі, що Ви не можете рухатися відразу за напрямками двох цих векторів і досягти відразу двох цілей. Вектори взаємодіють, або, якщо говорити математичною мовою, над векторами проводиться деяка операція. Результатом цієї операції стає вектор "Результат", який призводить Вас до Мети 3.

А тепер скажіть: результатом якої операції над векторами "Предприимчивость" і "Інноваційні здібності" є вектор "Результат"? Якщо не можете сказати відразу, не сумуйте. У міру вивчення цього уроку Ви зможете відповісти на це питання.

Як ми вже побачили вище, вектор обов'язково йде від деякої точки A по прямій до деякої точці B. Отже, кожен вектор має не тільки числове значення - довжину, але також фізичне і геометричне - спрямованість. З цього виводиться найперше, найпростіше визначення вектора. Отже, вектор - це спрямований відрізок, йде від точки A до точки B. Позначається він так:.

А щоб приступити до різних операціями з векторами , Нам потрібно познайомитися з ще одним визначенням вектора.

Вектор - це вид уявлення точки, до якої потрібно дістатися з деякою початкової точки. Наприклад, тривимірний вектор, як правило, записується у вигляді (х, y, z) . Говорячи зовсім просто, ці цифри означають, як далеко потрібно пройти в трьох різних напрямках, щоб дістатися до точки.

Нехай дано вектор. При цьому x = 3 (Права рука вказує направо), y = 1 (Ліва рука вказує вперед), z = 5 (Під точкою варто сходи, що ведуть нагору). За цими даними ви знайдете точку, проходячи 3 метра в напрямку, що вказується правою рукою, потім 1 метр в напрямку, що вказується лівою рукою, а далі Вас чекає сходи і, піднімаючись на 5 метрів, Ви, нарешті, опинитеся в кінцевій точці.

Всі інші терміни - це уточнення представленого вище пояснення, необхідні для різних операцій над векторами, тобто, рішення практичних завдань. Пройдемося по цим більш суворим визначенням, зупиняючись на типових задачах на вектори.

фізичними прикладами векторних величин можуть служити зміщення матеріальної точки, що рухається в просторі, швидкість і прискорення цієї точки, а також діюча на неї сила.

геометричний вектор представлений в двовимірному і тривимірному просторі у вигляді спрямованого відрізка. Це відрізок, у якого розрізняють початок і кінець.

якщо A - початок вектора, а B - його кінець, то вектор позначається символом або однієї малої буквою. На малюнку кінець вектора вказується стрілкою (рис. 1)

довжиною (або модулем) Геометричного вектора називається довжина породжує його відрізка

Два вектора називаються рівними , Якщо вони можуть бути суміщені (при збігу напрямків) шляхом паралельного перенесення, тобто якщо вони паралельні, спрямовані в одну і ту ж сторону і мають рівні довжини.

У фізиці часто розглядаються закріплені вектори, Задані точкою докладання, довжиною і напрямком. Якщо точка докладання вектора не має значення, то його можна переносити, зберігаючи довжину і напрямок в будь-яку точку простору. У цьому випадку вектор називається вільним. Ми домовимося розглядати тільки вільні вектори.

Лінійні операції над геометричними векторами

Множення вектора на число

твором вектора на число називається вектор, що виходить з вектора розтягуванням (при) або стисненням (при) в раз, причому напрям вектора зберігається, якщо, і змінюється на протилежне, якщо. (Рис. 2)

З визначення випливає, що вектори і \u003d завжди розташовані на одній або на паралельних прямих. Такі вектори називаються колінеарними. (Можна говорити також, що ці вектори паралельні, проте в векторній алгебрі прийнято говорити "колінеарні".) Справедливо і зворотне твердження: якщо вектори і колінеарні, то вони пов'язані ставленням

Отже, рівність (1) висловлює умова коллинеарности двох векторів.

Додавання і віднімання векторів

При додаванні векторів потрібно знати, що сумою векторів і називається вектор, початок якого збігається з початком вектора, а кінець - з кінцем вектора, за умови, що початок вектора докладено до кінця вектора. (Рис. 3)

Це визначення може бути розподілено на будь-яке кінцеве число векторів. Нехай в просторі дані n вільних векторів. При додаванні декількох векторів за їх суму приймають замикає вектор, початок якого збігається з початком першого вектора, а кінець - з кінцем останнього вектора. Тобто, якщо до кінця вектора докласти початок вектора, а до кінця вектора - початок вектора і т.д. і, нарешті, до кінця вектора - початок вектора, то сумою цих векторів служить замикає вектор , Початок якого збігається з початком першого вектора, а кінець - з кінцем останнього вектора. (Рис. 4)

Складові називаються складовими вектора, а сформульоване правило - правилом багатокутника. Цей багатокутник може і не бути плоским.

При множенні вектора на число -1 виходить протилежний вектор. Вектори і мають однакові довжини і протилежні напрямки. Їх сума дає нульовий вектор, Довжина якого дорівнює нулю. Напрямок нульового вектора не визначене.

У векторній алгебрі немає необхідності розглядати окремо операцію віднімання: відняти з вектора вектор означає додати до вектора протилежний вектор, тобто

Приклад 1. Спростити вираз:

.

,

тобто, вектори можна складати і множити на числа так само, як і многочлени (зокрема, також завдання на спрощення виразів). Зазвичай необхідність спрощувати лінійно подібні вирази з векторами виникає перед обчисленням творів векторів.

Приклад 2. Вектори і служать діагоналями паралелограма ABCD (рис. 4а). Висловити через та вектори,, і, що є сторонами цього паралелограма.

Рішення. Точка перетину діагоналей паралелограма ділить кожну діагональ навпіл. Довжини необхідних в умові завдання векторів знаходимо або як половини сум векторів, що утворюють з шуканими трикутник, або як половини різниць (в залежності від напрямку вектора, службовця діагоналлю), або, як в останньому випадку, половини суми, взятої зі знаком мінус. Результат - необхідні в умові завдання вектори:

Є всі підстави вважати, що тепер Ви правильно відповіли на питання про вектори "Предприимчивость" і "Інноваційні здібності" на початку цього уроку. Правильна відповідь: над цими векторами проводиться операція додавання.

Вирішити завдання на вектори самостійно, а потім подивитися рішення

Як знайти довжину суми векторів?

Це завдання займає особливе місце в операціях з векторами, так як передбачає використання тригонометричних властивостей. Припустимо, Вам попалася завдання на зразок наступної:

Дано довжини векторів і довжина суми цих векторів. Знайти довжину різниці цих векторів.

Рішення цієї та інших подібних завдань і пояснення, як їх вирішувати - в уроці " Сума векторів: довжина суми векторів і теорема косинусів ".

А перевірити рішення таких задач можна на Калькуляторі онлайн "Невідома сторона трикутника (додавання векторів і теорема косинусів)" .

А де твори векторів?

Твори вектора на вектор не є лінійними операціями і розглядаються окремо. І у нас є уроки "Скалярний добуток векторів" і "Векторное і змішане твори векторів".

Проекція вектора на вісь

Проекція вектора на вісь дорівнює добутку довжини проектованого вектора на косинус кута між вектором і віссю:

Як відомо, проекцією точки A на пряму (площину) служить підставу перпендикуляра, опущеного з цієї точки на пряму (площину).

Нехай - довільний вектор (Рис. 5), а й - проекції його початку (точки A) І кінця (точки B) На вісь l. (Для побудови проекції точки A) На пряму проводимо через точку A площину, перпендикулярну прямій. Перетин прямої і площини визначить необхідну проекцію.

складової вектора на осі l називається такий вектор, що лежить на цій осі, початок якого збігається з проекцією початку, а кінець - з проекцією кінця вектора.

Проекцією вектора на вісь l називається число

,

яка дорівнює довжині становить вектора на цій осі, взяте зі знаком плюс, якщо напрямок составляюшей збігається з напрямком осі l, І зі знаком мінус, якщо ці напрямки протилежні.

Основні властивості проекцій вектора на вісь:

1. Проекції рівних векторів на одну і ту ж вісь рівні між собою.

2. При множенні вектора на число його проекція множиться на це ж число.

3. Проекція суми векторів на якусь вісь дорівнює сумі проекцій на цю ж вісь доданків векторів.

4. Проекція вектора на вісь дорівнює добутку довжини проектованого вектора на косинус кута між вектором і віссю:

.

Рішення. Спроектуємо вектори на вісь l як визначено в теоретичній довідці вище. З рис.5а очевидно, що проекція суми векторів дорівнює сумі проекцій векторів. Обчислюємо ці проекції:

Знаходимо остаточну проекцію суми векторів:

Зв'язок вектора з прямокутної декартової системою координат в просторі

Знайомство із прямокутної декартової системою координат в просторі відбулося в відповідному уроці , Бажано відкрити його в новому вікні.

У впорядкованій системі координатних осей 0xyz вісь Ox називається віссю абсцис, вісь 0y – віссю ординат, І вісь 0z – віссю аплікат.

З довільної точкою М простору зв'яжемо вектор

званий радіус-векторомточки Мі спроеціруем його на кожну з координатних осей. Позначимо величини відповідних проекцій:

числа x, y, zназиваються координатами точки М, відповідно абсциссой, ординатою і аплікатою, І записуються у вигляді впорядкованої точки чисел: M (x; y; z) (Рис.6).

Вектор одиничної довжини, напрямок якого збігається з напрямком осі, називають одиничним вектором(або ортом) Осі. позначимо через

Відповідно орти координатних осей Ox, Oy, Oz

Теорема. Всякий вектор може бути розкладений по ортам координатних осей:

(2)

Рівність (2) називається розкладанням вектора по координатним осях. Коефіцієнтами цього розкладання є проекції вектора на координатні осі. Таким чином, коефіцієнтами розкладання (2) вектора по координатним осях є координати вектора.

Після вибору в просторі певної системи координат вектор і трійка його координат однозначно визначають один одного, тому вектор може бути записаний у формі

Уявлення вектора у вигляді (2) і (3) тотожні.

Умова коллинеарности векторів в координатах

Як ми вже відзначали, вектори називаються колінеарними, якщо вони пов'язані ставленням

Нехай дано вектори . Ці вектори колінеарні, якщо координати векторів пов'язані ставленням

,

тобто, координати векторів пропорційні.

Приклад 6. дано вектори . Колінеарні ці вектори?

Рішення. З'ясуємо співвідношення координат даних векторів:

.

Координати векторів пропорційні, отже, вектори колінеарні, або, що те ж саме, паралельні.

Довжина вектора і напрямні косинуси

Внаслідок взаємної перпендикулярності координатних осей довжина вектора

дорівнює довжині діагоналі прямокутного паралелепіпеда, побудованого на векторах

і виражається рівністю

(4)

Вектор повністю визначається завданням двох точок (початку і кінця), тому координати вектора можна виразити через координати цих точок.

Нехай в заданій системі координат початок вектора знаходиться в точці

а кінець - в точці

з рівності

Випливає, що

або в координатній формі

отже, координати вектора дорівнюють різницям однойменних координат кінця та початку вектора . Формула (4) в цьому випадку набуде вигляду

Напрямок вектора визначають направляючі косинуси . Це косинуси кутів, які вектор утворює з осями Ox, Oy і Oz. Позначимо ці кути відповідно α , β і γ . Тоді косинуси цих кутів можна знайти за формулами

Направляючі косинуси вектора є також координатами орта цього вектора і, таким чином, орт вектора

.

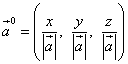
З огляду на, що довжина орта вектора дорівнює одній одиниці, тобто

,

отримуємо наступне рівність для напрямних косинусів:

Приклад 7.Знайти довжину вектора x = (3; 0; 4).

Рішення. Довжина вектора дорівнює

Приклад 8.Дано точки:

З'ясувати, рівнобедрений трикутник, побудований на цих точках.

Рішення. За формулою довжини вектора (6) знайдемо довжини сторін і встановимо, чи є серед них дві рівні:

Дві рівні сторони знайшлися, отже необхідність шукати довжину третьої сторони відпадає, а заданий трикутник є рівнобедреним.

Приклад 9. Знайти довжину вектора і його напрямні косинуси, якщо .

Рішення. Координати вектора дані:

.

Довжина вектора дорівнює квадратному кореню з суми квадратів координат вектора:

.

Знаходимо напрямні косинуси:

Вирішити завдання на вектори самостійно, а потім подивитися рішення

Операції над векторами, заданими в координатної формі

Нехай дано два вектора і, задані своїми проекціями:

Зазначимо дії над цими векторами.

1. Знаходження проекцій геометрично.

вектор
- проекція вектора на вісь OX
- проекція вектора на вісь OY

Визначення 1. проекцією вектора на будь-яку вісь координат називається взяте зі знаком "плюс" або "мінус" число, відповідне довжині відрізка, розташованого між підставами перпендикулярів, опущених з початку і кінця вектора на вісь координат.

Знак проекції визначається так. Якщо при русі вздовж осі координат відбувається переміщення від точки проекції початку вектора до точки проекції кінця вектора в позитивному напрямку осі, то проекція вектора вважається позитивною. Якщо ж - протилежно осі, то проекція вважається негативною.

За малюнком видно, що якщо вектор орієнтований якось протилежно осі координат, то його проекція на цю вісь негативна. Якщо вектор орієнтований якось в позитивному напрямку осі координат, то його проекція на цю вісь позитивна.

Якщо вектор перпендикулярний осі координат, то його проекція на цю вісь дорівнює нулю.
Якщо вектор сонаправлени з віссю, то його проекція на цю вісь дорівнює модулю вектора.
Якщо вектор протилежно спрямований осі координат, то його проекція на цю вісь по абсолютній величині дорівнює модулю вектора, взятому зі знаком мінус.

2. Найбільш загальне визначення проекції.

З прямокутного трикутника ABD: .

Визначення 2. проекцією вектора на будь-яку вісь координат називається число, яке дорівнює добутку модуля вектора і косинуса кута, утвореного вектором з позитивним напрямком осі координат.

Знак проекції визначається знаком косинуса кута, утвореного вектором з позитивним напрямком осі.
Якщо кут гострий, то косинус має позитивний знак, і проекції - позитивні. Для тупих кутів косинус має негативний знак, тому в таких випадках проекції на вісь негативні.
- тому для векторів, перпендикулярних до осі, проекція дорівнює нулю.

З фізики за 9 клас (І.К.Кікоін, А.К.Кікоін, 1999 год),
задача №5
до глави « ГЛАВА 1. ЗАГАЛЬНІ ВІДОМОСТІ ПРО РУХ».

1. Що називають проекцією вектора на координатну вісь?

1. проекцією вектора а на координатну вісь називають довжину відрізка між проекціями початку і кінця вектора а (перпендикулярами, опущеними з цих точок на вісь) на цю координатну вісь.

2. Як пов'язаний вектор переміщення тіла з його координатами?

2. Проекції вектора переміщення s на осі координат дорівнюють зміни відповідних координат тіла.

3. Якщо координата точки з плином часу збільшується, то який знак має проекція вектора переміщення на координатну вісь? А якщо вона зменшується?

3. Якщо координата точки з плином часу збільшується, то проекція вектора переміщення на координатну вісь буде позитивною, тому що в цьому випадку ми будемо йти від проекції початку до проекції кінця вектора у напрямку самої осі.

Якщо координата точки з плином часу буде зменшуватися, то проекція вектора переміщення на координатну вісь буде негативною, тому що в цьому випадку ми будемо йти від проекції початку до проекції кінця вектора проти направляючої самої осі.

4. Якщо вектор переміщення паралельний осі X, то чому дорівнює модуль проекції вектора на цю вісь? А модуль проекції цього ж вектора на вісь У?

4. Якщо вектор переміщення паралельний осі Х, то модуль проекції вектора на цю вісь дорівнює модулю самого вектора, а його проекція на вісь Y дорівнює нулю.

5. Визначте знаки проекцій на вісь X векторів переміщення, зображених на малюнку 22. Як при цих переміщеннях змінюються координати тіла?

5. У всіх нижченаведених випадках координата Y тіла не змінюється, а координата Х тіла буде змінюватися наступним чином:

a) s 1;

проекція вектора s 1, на вісь Х негативна і по модулю дорівнює довжині вектора s 1. При такому переміщенні координата Х тіла зменшиться на довжину вектора s 1.

b) s 2;

проекція вектора s 2 на вісь X позитивна і дорівнює по модулю довжині вектора s 1. При такому переміщенні координата Х тіла збільшиться на довжину вектора s 2.

c) s 3;

проекція вектора s 3 на вісь Х негативна і дорівнює по модулю довжині вектора s 3. При такому переміщенні координата Х тіла зменшиться на довжину вектора s 3.

d) s 4;

проекція вектора s 4 на вісь X позитивна і дорівнює по модулю довжині вектора s 4. При такому переміщенні координата Х тіла збільшиться на довжину вектора s 4.

e) s 5;

проекція вектора s 5 на вісь Х негативна і дорівнює по модулю довжині вектора s 5. При такому переміщенні координата Х тіла зменшиться на довжину вектора s 5.

6. Якщо значення пройденого шляху велике, то чи може модуль переміщення бути малим?

6. Чи може. Це пов'язано з тим, що переміщення (вектор переміщення) є векторною величиною, тобто являє собою спрямований відрізок прямої, що сполучає початкове положення тіла з його подальшими положеннями. А кінцеве положення тіла (незалежно від величини пройденого шляху) може знаходитися як завгодно близько до початкового стану тіла. У разі збігу кінцевого і початкового положень тіла, модуль переміщення дорівнюватиме нулю.

7. Чому в механіці важливіший вектор переміщення тіла, ніж пройдений їм шлях?

7. Основним завданням механіки є визначення положення тіла в будь-який момент часу. Знаючи вектор переміщення тіла ми можемо визначити координати тіла, тобто положення тіла в будь-який момент часу, а знаючи тільки пройдений шлях ми не можемо визначити координати тіла, тому що ми не маємо відомостей про напрямок руху, а можемо тільки судити про довжину пройденого шляху на даний момент часу.

Пр a b \u003d | b | cos (a, b) або

Де a b - скалярний добуток векторів, | a | - модуль вектора a.

Інструкція. Для знаходження проекції вектора пp a b в онлайн режимі необхідно вказати координати векторів a і b. При цьому вектор може бути заданий на площині (дві координати) і в просторі (три координати). Отримане рішення зберігається в файлі Word. Якщо вектори задані через координати точок, то необхідно використовувати цей калькулятор.

Класифікація проекцій вектора

Види проекцій за визначенням проекція вектора

1. Геометрична проекція вектора AB на вісь (вектор) називається вектор A "B", початок якого A 'є проекція початку A на вісь (вектор), а кінець B' - проекція кінця B на ту ж вісь.
2. Алгебраїчна проекція вектора AB на вісь (вектор) називається довжина вектора A "B", взята зі знаком + або -, в залежності від того, чи має вектор A "B" той самий напрямок, що і вісь (вектор).

Види проекцій по системі координат

Властивості проекції вектора

1. Геометрична проекція вектора є вектор (має напрямок).
2. Алгебраїчна проекція вектора є число.

Теореми про проекціях вектора

AC "\u003d AB" + B "C"

Пр a b \u003d | b | · cos (a, b)

Види проекцій вектора

1. проекція на вісь OX.
2. проекція на вісь OY.
3. проекція на вектор.

Проекція на вісь OX	Проекція на вісь OY	Проекція на вектор
Якщо напрямок вектора A'B 'збігається з напрямком осі OX, то проекція вектора A'B' має позитивний знак.	Якщо напрямок вектора A'B 'збігається з напрямком осі OY, то проекція вектора A'B' має позитивний знак.	Якщо напрямок вектора A'B 'збігається з напрямком вектора NM, то проекція вектора A'B' має позитивний знак.
Якщо напрямок вектора протилежно до напрямку осі OX, то проекція вектора A'B 'має негативний знак.	Якщо напрямок вектора A'B 'протилежно до напрямку осі OY, то проекція вектора A'B' має негативний знак.	Якщо напрямок вектора A'B 'протилежно до напрямку вектора NM, то проекція вектора A'B' має негативний знак.
Якщо вектор AB паралельний осі OX, то проекція вектора A'B 'дорівнює модулю вектора AB.	Якщо вектор AB паралельний осі OY, то проекція вектора A'B 'дорівнює модулю вектора AB.	Якщо вектор AB паралельний вектору NM, то проекція вектора A'B 'дорівнює модулю вектора AB.
Якщо вектор AB перпендикулярний осі OX, то проекція A'B 'дорівнює нулю (нуль-вектор).	Якщо вектор AB перпендикулярний осі OY, то проекція A'B 'дорівнює нулю (нуль-вектор).	Якщо вектор AB перпендикулярний вектору NM, то проекція A'B 'дорівнює нулю (нуль-вектор).

1. Питання: Чи може проекція вектора мати негативний знак. Відповідь: Так, проекцій вектора може бути негативною величиною. В цьому випадку, вектор має протилежний зміст (див. Як спрямовані вісь OX і вектор AB)
2. Питання: Чи може проекція вектора збігатися з модулем вектора. Відповідь: Так, може. В цьому випадку, вектори паралельні (або лежать на одній прямій).
3. Питання: Чи може проекція вектора дорівнювати нулю (нуль-вектор). Відповідь: Так, може. У цьому випадку вектор перпендикулярний відповідної осі (вектору).

Приклад 1. Вектор (рис. 1) утворює з віссю OX (вона задана вектором a) кут 60 о. Якщо OE є одиниця масштабу, то | b | \u003d 4, так що .

Дійсно, довжина вектора (геометричної проекції b) дорівнює 2, а напрямок збігається з напрямком осі OX.

Приклад 2. Вектор (рис. 2) утворює з віссю OX (з вектором a) кут (a, b) \u003d 120 o. Довжина | b | вектора b дорівнює 4, тому пр a b \u003d 4 · cos120 o \u003d -2.

Дійсно, довжина вектора дорівнює 2, а напрям протилежний напрямку осі.